[Paper Review] 2019_[AAAI]Multi-agent pathfinding: Definitions, variants, and benchmarks

 

 

Abstract 정리

멀티 에이전트 경로 계획(MAPF) 문제는 여러 에이전트의 경로를 계획하는 기본적인 문제로, 핵심 제약 조건은 에이전트들이 서로 충돌하지 않으면서 이러한 경로를 동시에 따를 수 있어야 한다는 것입니다. MAPF의 응용 분야로는 자동화된 창고와 자율 주행 차량 등이 있습니다. 최근 몇 년간 MAPF에 대한 연구가 활발히 이루어지고 있습니다. 다양한 MAPF 연구 논문들은 서로 다른 가정 (기존 논문들을 이해하기 어려운 이유)을 하고 있습니다. 예를 들면, 에이전트들이 동시에 같은 길을 지나갈 수 있는지 여부, 그리고 다른 목표 함수들, 예를 들어 작업 시간 최소화 또는 에이전트들의 행동 비용 합 최소화 등이 있습니다. 이러한 가정과 목표들은 때때로 묵시적으로 가정되거나 비공식적으로 설명됩니다. 이는 연구 논문들에서 적절한 기준을 설정하는 것을 어렵게 만들며, 실무자들이 그들의 구체적인 응용 분야에 관련된 논문을 찾는 것도 어렵게 만듭니다. 이 논문은 공통적인 MAPF 가정과 목표를 설명하기 위한 통합 용어를 제공함으로써 연구자들과 실무자들을 지원하려는 목적 (이 논문의 목적)을 가지고 있습니다. 또한, 우리는 MAPF 벤치마크 두 개에 대한 정보도 제공합니다. 특히, 우리는 새로운 그리드 기반 MAPF 벤치마크를 소개하고, 현대 MAPF 알고리즘들에게 도전이 될 수 있음을 실험적으로 보여줍니다.

---

Introduction 정리

MAPF(Multi-Agent Pathfinding)는 여러 에이전트에 대한 경로를 계획하는 중요한 다중 에이전트 계획 문제입니다. 여기서 핵심 제약 조건은 에이전트들이 서로 충돌하지 않으면서 이 경로들을 동시에 따를 수 있어야 한다는 것입니다. MAPF는 자동화된 창고, 자율 주행 차량, 로보틱스 등 현대의 다양한 응용 분야에 중요합니다. 그 결과, 최근 몇 년간 다양한 연구 그룹과 학술 커뮤니티들이 이 문제에 주목하고 있습니다 (Standley 2010; Felner et al. 2017; Surynek et al. 2016; Barták, Švancara, Vlk 2018; Cohen et al. 2018a; Li et al. 2019; Ma et al. 2019a).

다양한 MAPF 연구 논문들은 에이전트에 대한 다른 가정들을 고려하고 서로 다른 목표를 추구 (기존 논문들을 이해하기 어려운 이유)합니다. 이러한 가정과 목표들은 때때로 묵시적으로 가정되거나 비공식적으로 설명됩니다. 가정과 목표 함수가 공식적으로 설명된 경우에도 사용되는 MAPF 용어에서 차이 (기존 논문들을 이해하기 어려운 이유)가 있습니다. 이는 기존 문헌을 이해하고 적절한 기준선을 설정하는 데 어려움을 줍니다. 또한, 실무자들이 그들의 구체적인 응용 분야에 관련된 논문을 찾는 것도 어렵게 만듭니다.

이 논문은 MAPF 문제들을 설명하기 위한 통합된 용어를 도입하고, MAPF 알고리즘을 평가하기 위한 공통 벤치마크와 평가 척도를 설정 (이 논문의 목적)함으로써 이러한 도전을 해결하려고 합니다. 이 논문에서 제시하는 통합된 MAPF 용어는 현재 연구되고 있는 MAPF 변형들을 분류하려는 우리의 시도입니다. 우리는 이 용어가 향후 연구자들에게 공통의 기반으로 사용되고, 그들의 기여를 간결하고 정확하게 설명하는 데 사용될 것이라고 기대합니다.

이 논문의 두 번째 부분에서는 새로운 그리드 MAPF 벤치마크를 커뮤니티에 소개 (이 논문의 또 다른 contribution)합니다. 이 벤치마크는 다양한 맵과 생성된 출발 및 목적지 정점을 포함합니다. 우리는 이 벤치마크에서 표준 MAPF 알고리즘의 성능을 보고하여 향후 연구를 위한 기준선으로 사용하고자 합니다. 이 벤치마크는 향후 연구자들을 돕고 기존 및 미래의 MAPF 알고리즘들에 대한 보다 과학적으로 엄격한 경험적 비교를 가능하게 하기 위한 것입니다. 이 벤치마크들이 완벽하지는 않다고 주장하지 않습니다. 그러나 이러한 벤치마크의 사용과 연구를 통해 발견되고 수정될 수 있는 편향성이 있을 수 있습니다. 또한 이 문서가 최신 MAPF 알고리즘에 대한 조사를 의도한 것이 아니라는 점을 강조하는 것이 중요합니다. (여기서 제공하는 resources: http://mapf.info)

---

2 Classical MAPF

우리가 고전적 MAPF(멀티 에이전트 경로 계획) 문제라고 부르는 것을 먼저 설명합니다. k명의 에이전트가 있는 고전적 MAPF 문제의 입력은 튜플 \(G, s, t\)로, 여기서 \(G = (V, E)\)는 무방향 그래프이며, \(s : [1, \ldots, k] \rightarrow V\)는 에이전트를 출발 정점에, \(t : [1, \ldots, k] \rightarrow V\)는 에이전트를 목표 정점에 매핑합니다. 시간은 이산화되어 가정되며, 각 시간 단계에서 각 에이전트는 그래프의 하나의 정점에 위치하고 단일 행동을 수행할 수 있습니다. 고전적 MAPF에서 행동은 \(a : V \rightarrow V\)와 같은 함수로서 \(a(v) = v'\)는 에이전트가 정점 \(v\)에 있고 \(a\)를 수행하면 다음 시간 단계에서 정점 \(v'\)에 있게 된다는 것을 의미합니다. 각 에이전트는 대기와 이동의 두 가지 유형의 행동을 가집니다. 대기 행동은 에이전트가 현재 정점에 다음 시간 단계까지 머무른다는 것을 의미합니다. 이동 행동은 에이전트가 현재 정점 \(v\)에서 그래프 내 인접한 정점 \(v'\)으로 이동한다는 것을 의미합니다(즉, \((v, v') \in E\)).

행동의 시퀀스 \(π = (a_1, \ldots, a_n)\)와 에이전트 \(i\)에 대해, 우리는 \(π_i[x]\)를 에이전트의 출발지 \(s(i)\)에서 시작하여 \(π\)의 첫 \(x\) 행동을 수행한 후 에이전트의 위치로 표시합니다. 공식적으로, \(π_i[x] = a_x(a_{x-1}(\ldots a_1(s(i))))\). 행동의 시퀀스 \(π\)는 에이전트 \(i\)에 대한 단일 에이전트 계획이며, 이 행동 시퀀스를 \(s(i)\)에서 실행하면 \(t(i)\)에 도달하는 것입니다. 즉, \(π_i[|π|] = t(i)\)입니다. 해결책은 각 에이전트마다 하나씩, \(k\)개의 단일 에이전트 계획 세트입니다.

 

2.1 Types of Conflicts in Classical MAPF

MAPF 솔버의 궁극적 목표는 충돌 없이 실행될 수 있는 해결책, 즉 각 에이전트를 위한 단일 에이전트 계획을 찾는 것입니다. 이를 달성하기 위해, MAPF 솔버는 계획 중에 충돌의 개념을 사용합니다. 여기서 MAPF 해결책은 어떤 두 단일 에이전트 계획 사이에도 충돌이 없는 경우에만 유효하다고 합니다. 충돌을 구성하는 것의 정의는 환경에 따라 다르며, 그에 따라 고전적 MAPF에 대한 문헌에서는 계획 사이의 충돌을 구성하는 것에 대한 여러 가지 다른 정의를 포함하고 있습니다. 아래에는 일반적인 충돌 정의를 나열합니다. \(π_i\)와 \(π_j\)를 단일 에이전트 계획의 한 쌍이라고 합시다.

• Vertex conflict: \(π_i\)와 \(π_j\) 사이에 정점 충돌이 발생하는 경우는 이 계획에 따라 에이전트들이 동일한 시간 단계에서 같은 정점을 차지하도록 계획된 경우입니다. 공식적으로, \(π_i\)와 \(π_j\) 사이에 정점 충돌이 있는 경우는 시간 단계 \(x\)가 존재하여 \(π_i[x] = π_j[x]\)인 경우입니다.
• Edge conflict: \(π_i\)와 \(π_j\) 사이에 변 충돌이 발생하는 경우는 이 계획에 따라 에이전트들이 동일한 시간 단계에서 동일한 방향으로 같은 변을 통과하도록 계획된 경우입니다. 공식적으로, \(π_i\)와 \(π_j\) 사이에 변 충돌이 있는 경우는 시간 단계 \(x\)가 존재하여 \(π_i[x] = π_j[x]\)이고 \(π_i[x+1] = π_j[x+1]\)인 경우입니다.
• Following conflict: \(π_i\)와 \(π_j\) 사이에 따라가기 충돌이 발생하는 경우는 한 에이전트가 이전 시간 단계에 다른 에이전트가 차지하고 있던 정점을 차지하도록 계획된 경우입니다. 공식적으로, \(π_i\)와 \(π_j\) 사이에 따라가기 충돌이 있는 경우는 시간 단계 \(x\)가 존재하여 \(π_i[x+1] = π_j[x]\)인 경우입니다.
• Cycle conflict: \(π_i, π_{i+1}, \ldots, π_j\)의 단일 에이전트 계획 세트 사이에 순환 충돌이 발생하는 경우는 동일한 시간 단계에서 모든 에이전트가 "회전 순환" 패턴을 형성하며 다른 에이전트가 이전에 차지하고 있던 정점으로 이동하는 경우입니다. 공식적으로, \(π_i, π_{i+1}, \ldots, π_j\)의 계획 세트 사이에 순환 충돌이 있는 경우는 시간 단계 \(x\)가 존재하며 \(π_i(x+1) = π_{i+1}(x)\)이고 \(π_{i+1}(x+1) = π_{i+2}(x)\), ... , \(π_{j-1}(x+1) = π_j(x)\)이고 \(π_j(x+1) = π_i(x)\)인 경우입니다.
• Swapping conflict: \(π_i\)와 \(π_j\) 사이에 위치 교환 충돌이 발생하는 경우는 에이전트들이 단일 시간 단계에서 위치를 교환하도록 계획된 경우입니다. 공식적으로, \(π_i\)와 \(π_j\) 사이에 위치 교환 충돌이 있는 경우는 시간 단계 \(x\)가 존재하여 \(π_i[x+1] = π_j[x]\)이고 \(π_j[x+1] = π_i[x]\)인 경우입니다. 이 충돌은 현재 MAPF 문헌에서 때때로 변 충돌이라고 불립니다.

위의 충돌 정의 세트는 모든 가능한 충돌의 완전한 세트는 아닙니다. 이 충돌들의 공식 정의를 고려할 때, 그들 사이에는 우선 순위 관계가 있음이 분명합니다: (1) 정점 충돌을 금지하면 변 충돌도 금지됩니다, (2) 따라가기 충돌을 금지하면 순환 충돌과 위치 교환 충돌도 금지됩니다, (3) 순환 충돌을 금지하면 위치 교환 충돌도 금지됩니다. 반대로, (1) 변 충돌을 허용하면 정점 충돌도 허용됩니다, (2) 위치 교환 충돌을 허용하면 순환 충돌도 허용됩니다, 그리고 (3) 순환 충돌을 허용하면 따라가기 충돌도 허용됩니다.

고전적 MAPF 문제를 적절히 정의하기 위해서는 해결책에서 허용되는 충돌 유형을 명시해야 합니다. 가장 제약이 적은 제한은 변 충돌만 금지하는 것입니다. 그러나 우리가 알고 있는 한, 고전적 MAPF에 대한 모든 이전 작업은 정점 충돌도 금지합니다. 일부 MAPF 작업은 위치 교환 충돌을 허용합니다(Ma et al. 2016). 대부분의 탐색 기반 MAPF 알고리즘 작업(Standley 2010; Felner et al. 2017)은 위치 교환 충돌을 금지하지만, 따라가기 충돌은 허용합니다. 컴파일 기반 MAPF 알고리즘 작업과 페블 모션 문제로 MAPF를 고려하는 모든 작업은 따라가기 충돌도 금지합니다 (Surynek et al. 2016; Barták et al. 2017). (기존 MAPF 방법론에서 정의하고 있는 충돌 유형과 금지/허용 하고 있는 충돌들에 대한 정리)

 

2.2 Agent Behavior at Target in Classical MAPF

고전적 MAPF 문제의 해결책에서, 에이전트는 다른 시간 단계에서 목표에 도달할 수 있습니다. 따라서 고전적 MAPF 문제를 정의할 때, 한 에이전트가 목표에 도달한 후 및 마지막 에이전트가 목표에 도달하기 전에 에이전트가 어떻게 행동하는지 정의해야 합니다. 에이전트가 목표에서 어떻게 행동하는지에 대해 두 가지 일반적인 가정이 있습니다.

• Stay at target: 이 가정하에, 에이전트는 모든 에이전트가 그들의 목표에 도달할 때까지 목표에서 대기합니다. 이 대기 중인 에이전트는 목표에 도달한 후 그 목표를 통과하는 어떤 계획과도 정점 충돌을 일으킬 것입니다. 공식적으로, 목표에 머무르기 가정하에, 단일 에이전트 계획의 한 쌍 \(π_i\)와 \(π_j\)는 시간 단계 \(t ≥ |π_i|\)가 존재하면 \(π_j[t] = π_i[|π_i|]\)인 경우 정점 충돌을 가집니다.
• Disappear at target: 이 가정하에, 에이전트가 목표에 도달하면 즉시 사라집니다. 이는 해당 에이전트의 계획이 해당 에이전트가 목표에 도달한 시간 단계 이후에는 어떠한 충돌도 가지지 않을 것임을 의미합니다.

대부분의 이전 고전적 MAPF 작업은 목표에 머무르기를 가정했지만, 최근의 작업은 목표에서 사라지기 가정도 고려했습니다(Ma et al. 2019a). (목적지에서 agent의 행동 결정)

 

2.3 Objective Functions in Classical MAPF

대부분의 실제 MAPF(멀티 에이전트 경로 계획) 응용에서, 일부 MAPF 솔루션은 다른 솔루션보다 더 낫다고 말하는 것이 안전합니다. 이를 포착하기 위해, 고전적 MAPF 작업은 MAPF 솔루션을 평가하는 데 사용되는 목적 함수를 고려합니다. 고전적 MAPF에서 솔루션을 평가하는 데 사용되는 두 가지 가장 일반적인 함수는 Makespan과 Sum of costs입니다.

• Makespan: 모든 에이전트가 그들의 목표에 도달하는 데 필요한 시간 단계의 수입니다. MAPF 솔루션 \(π = \{π_1, \ldots, π_k\}\)에 대해, \(π\)의 메이크스팬은 \(max_{1≤i≤k} |π_i|\)로 정의됩니다.
• Sum of costs: 각 에이전트가 목표에 도달하는 데 필요한 시간 단계의 합입니다. \(π\)의 비용 합은 \(∑_{1≤i≤k} |π_i|\)로 정의됩니다. 비용의 합은 또한 플로우타임으로 알려져 있습니다.

목표에 머무르는 에이전트 행동이 목표에 머무르기이고 목적 함수가 비용의 합이라면, 목표에 머무르는 것이 비용의 합에 어떤 영향을 미치는지 명시해야 합니다. 예를 들어, 에이전트가 목표에서 대기하면 비용의 합을 증가시키지 않는다고 정의할 수 있습니다. 대부분의 이전 작업에서의 일반적인 가정은 에이전트가 다시 목표에서 움직일 계획이 없는 한 목표에 머무는 것이 대기 행동으로 간주된다는 것입니다. 예를 들어, 에이전트 \(i\)가 시간 단계 \(t\)에 목표에 도달하고, 시간 단계 \(t'\)에 목표를 떠나고, 시간 단계 \(t''\)에 다시 목표에 도착하여 모든 에이전트가 목표에 도달할 때까지 목표에 머무른다고 가정합니다. 그러면 이 단일 에이전트 계획은 해당 솔루션의 비용 합에 \(t''\)를 기여할 것입니다.

이것들이 고전적 MAPF에 대한 유일한 가능한 목적 함수라고 주장하지는 않습니다. 목표에 도달하기 위해 필요한 비대기 행동의 총합(일부는 이를 연료의 합 (sum-of-fuel)이라고 함)과 목표가 아닌 곳에서 에이전트가 보낸 총 시간과 같은 다른 목적 함수를 정의할 수 있습니다. 그러나, 우리가 알고 있는 한, 위의 목적 함수들은 고전적 MAPF에 대한 이전 작업에서 사용된 유일한 것들입니다. 메이크스팬은 컴파일 기반 MAPF 알고리즘에 의해 광범위하게 사용되었으며, 비용의 합은 대부분의 검색 기반 MAPF 알고리즘에 의해 사용되었습니다. 그러나, 두 유형의 MAPF 알고리즘 모두에 의해 두 목적 함수에 대한 작업이 있었습니다(Surynek et al. 2016). 주어진 메이크스팬(즉, 마감일) 내에 목표에 도달하는 에이전트 수를 최대화하는 작업도 있었습니다(Ma et al. 2018). (기존 방법론들의 목적함수 들; 주로 목표에 도달하는데 필요한 시간 (마감일:due)를 사용하거나 sum of costs를 사용)

---

3 Beyond Classical MAPF

위의 모든 고전적 MAPF 변형은 다음과 같은 가정을 공유합니다: (1) 시간은 시간 단계로 이산화됩니다, (2) 모든 행동은 정확히 하나의 시간 단계를 소요합니다, 그리고 (3) 모든 시간 단계에서, 각 에이전트는 정확히 하나의 정점을 차지합니다. (기존 방법론들의 가정들) 다음으로, 이러한 가정을 완화하는 몇 가지 MAPF 변형을 간략히 나열합니다.

3.1 MAPF on Weighted Graphs

이동 또는 대기와 같은 각 행동이 정확히 하나의 시간 단계를 소요한다는 가정은 에이전트의 다소 단순화된 동작 모델을 암시적으로 가정합니다. MAPF 문헌에서는 다른 행동이 다른 지속 시간을 가질 수 있는 더 복잡한 동작 모델 (새로운 가정)이 연구되었습니다. 이는 에이전트가 차지할 수 있는 가능한 위치를 나타내는 기본 그래프(앞서 G로 표시됨)가 이제 각 변의 가중치가 에이전트가 이 변을 통과하는 데 걸리는 시간을 나타내는 가중치 그래프라는 것을 의미 (새로운 가정을 나타내는 방법)합니다. Bartak et al. (2018)은 가중치 그래프 상의 MAPF에 대한 스케줄링 기반 접근 방식을 제안했고, Walker et al. (2018)은 증가 비용 트리 검색(ICTS) 알고리즘의 변형을 제안했습니다. Yakovlev와 Andreychuk (2017)은 SIPP 알고리즘(Phillips와 Likhachev 2011)과 우선 순위 계획의 하이브리드를 가중치 그래프에 대해 제안했습니다.

MAPF 연구에서 지금까지 사용된 가중치 그래프 유형은 다음을 포함합니다:

• MAPF in $2^k$ -neighbor grids: 이러한 맵은 모든 정점이 이차원 그리드의 셀을 나타내는 가중치 그래프의 제한된 형태입니다. 셀 내의 에이전트 이동 행동은 \(k\)가 매개변수인 모든 \(2^k\) 이웃 셀입니다. 비용은 유클리드 거리에 기반하여, \(k > 2\)일 때, 다른 비용을 가진 행동을 도입합니다. 예를 들어, 8-이웃 그리드에서 대각선 이동 비용은 $\sqrt{2}$이고 기본 방향 중 하나로의 이동 비용은 1입니다. 그림 2는 \(k = 2, 3, 4, 5\)에 대한 \(2^k\)-이웃 그리드에서 가능한 이동 행동을 보여줍니다.
• MAPF in Euclidean space: 유클리드 공간에서의 MAPF는 \(G\)의 모든 노드가 유클리드 점 \((x, y)\)를 나타내고 변이 허용된 이동 행동을 나타내는 MAPF의 일반화입니다. 이러한 설정은 예를 들어, 연속적인 유클리드 환경에 대해 생성된 도로맵이 기본 그래프인 경우에 발생합니다(Khatib 1986; Wagner, Kang, Choset 2012).

3.2 Feasibility Rules

고전적 MAPF에서 사용되는 유효한 해결책의 정의 - 충돌 없음 -는 솔루션 요구 사항의 한 유형일 뿐입니다. 우리는 MAPF 솔루션에 대한 요구 사항을 나타내는 용어로 '실행 가능성 규칙'이라는 용어를 사용합니다. 다른 MAPF 실행 가능성 규칙도 제안되었습니다.

• Robustness rules: 이 규칙은 MAPF 솔루션이 실행 중 예기치 않은 지연을 고려하도록 설계되었습니다. k-견고한 MAPF 계획은 에이전트가 최대 k 시간 단계까지 지연되어도 충돌이 발생하지 않도록 충분한 버퍼를 구축합니다 (Atzmon et al. 2018). 미래의 지연 가능성이 알려져 있을 때, 견고성 규칙은 에이전트가 실행 중에 충돌할 확률이 주어진 한계보다 낮을 것을 요구할 수 있습니다 (Wagner and Choset 2017) 또는 충돌 없는 실행을 보장하기 위해 실행 정책과 결합될 수 있습니다 (Ma, Kumar, and Koenig 2017).
• Formation rules: 이는 다른 에이전트의 위치에 따라 달라지지만 충돌과 관련이 없는 에이전트의 허용된 이동 행동에 대한 제한입니다. 예를 들어, 에이전트가 지정된 편대를 유지하도록 의도된 제한 (Barel, Manor, and Bruckstein 2017) 또는 일련의 이웃 에이전트와의 통신 링크를 유지하도록 의도된 제한 (Stump et al. 2011; Gilboa, Meisels, and Felner 2006)이 있습니다.
  
  

3.3 From Pathfinding to Motion Planning

고전적 MAPF에서 에이전트는 정확히 하나의 정점을 차지하며, 볼륨, 형태가 없고 일정한 속도로 이동한다고 가정됩니다. 반면에, 모션 플래닝 알고리즘은 이러한 속성을 직접 고려합니다. 여기서 에이전트는 각 시간 단계에서 단순히 정점이 아닌 구성에서 위치하며, 구성은 에이전트의 위치, 방향, 속도 등을 지정하고 구성 간의 변은 운동학적 움직임을 나타냅니다. 여러 주목할만한 MAPF 변형은 고전적 MAPF와 모션 플래닝 사이의 이러한 격차를 줄이는 단계입니다.

• MAPF with large agents: 일부 MAPF 연구는 특정 기하학적 형태와 부피를 가진 에이전트를 고려했습니다 (Li et al. 2019; Walker, Sturtevant, and Felner 2018; Yakovlev and Andreychuk 2017; Thomas, Deodhare, and Murty 2015). 에이전트가 부피를 가지고 있다는 사실은 기본 그래프 G에 에이전트가 어떻게 위치하고 그것에서 어떻게 움직이는지에 대한 질문을 제기합니다. 특히, 에이전트가 한 정점에 위치한다면, 다른 에이전트가 인근 정점을 차지하는 것을 금지할 수 있습니다.
   마찬가지로, 에이전트가 한 변을 따라 이동한다면, 다른 에이전트가 교차하는 변을 따라 이동하거나 변에 너무 가까운 정점에 머무르는 것을 금지할 수 있습니다. 이는 정점 대 정점, 변 대 변, 변 대 정점 충돌과 같은 새로운 유형의 충돌을 도입할 수 있습니다 (Hönig et al. 2018).
• MAPF with kinematic constraints: 다른 MAPF 연구에서는 에이전트의 이동 행동에 대한 운동학적 제약 조건을 고려했습니다 (Hönig et al. 2017; Walker, Chan, and Sturtevant 2017). 즉, 에이전트가 수행할 수 있는 이동 행동은 현재 위치뿐만 아니라 속도와 방향과 같은 상태 매개변수에도 의존합니다. 이러한 제약 조건의 부산물은 기본 그래프가 방향성을 가지게 되며, 에이전트의 운동학적 제약으로 인해 한 방향으로만 통과 가능한 변이 있을 수 있습니다. MAPF-POST는 예시로, MAPF 알고리즘에 의해 생성된 솔루션을 사후 처리하여 이러한 운동학적 제약을 고려하는 MAPF 알고리즘입니다. 회전 행동을 반 운동학적 제약으로 가정하는 감소 기반 접근 방식도 있습니다 (Barták et al. 2018).

3.4 Tasks and Agents

고전적 MAPF에서 각 에이전트는 하나의 과제를 가집니다 - 목표까지 가기. MAPF 문헌에서는 에이전트가 하나 이상의 목표를 할당받을 수 있는 여러 확장이 이루어졌습니다.

• Anonymous MAPF: 이 MAPF 변형에서 목표는 에이전트를 일련의 목표 정점으로 이동시키는 것이지만, 어떤 에이전트가 어떤 목표에 도달하는지는 중요하지 않습니다 (Kloder and Hutchinson 2006; Yu and LaValle 2013). 이 MAPF 변형을 다른 방식으로 보면, 모든 에이전트가 어떤 목표에도 할당될 수 있지만, 에이전트와 목표 사이에 일대일 매핑이 있어야 하는 MAPF 문제입니다.
• Colored MAPF: 이 MAPF 변형은 에이전트가 팀으로 그룹화되고, 각 팀에 목표 세트가 있으며, 각 팀의 에이전트를 그들의 목표로 이동시키는 것을 목표로 하는 익명 MAPF의 일반화입니다 (Ma and Koenig 2016; Solovey and Halperin 2014). 이 MAPF 변형을 다른 방식으로 보면, 모든 에이전트는 자신의 팀에 지정된 목표 세트에서만 목표에 할당될 수 있는 MAPF 문제입니다.
• Online MAPF: 온라인 MAPF에서는 동일한 그래프에서 MAPF 문제 시퀀스가 해결됩니다. 이 설정은 "Lifelong MAPF"(Ma et al. 2017; 2019b)라고도 불립니다. 온라인 MAPF 문제는 다음과 같이 분류될 수 있습니다.
  
  • Warehouse model: 에이전트가 MAPF 문제를 해결하는 고정된 세트가 있지만, 에이전트가 목표를 찾은 후 다른 목표로 이동해야 할 수도 있습니다 (Ma et al. 2019b). 이 설정은 자율 창고용 MAPF에서 영감을 받았습니다.
  • Intersection model: 새로운 에이전트가 나타날 수 있고, 각 에이전트는 하나의 과제 - 목표에 도달하기 - 를 가집니다 (Švancara et al. 2019). 이 설정은 자율 차량이 교차로에 진입하고 빠져나가는 것에서 영감을 받았습니다 (Dresner and Stone 2008). 

물론, 에이전트가 목표에 도달했을 때 새로운 과제를 받고 시간이 지남에 따라 새로운 에이전트가 나타날 수 있는 하이브리드 모델도 가능합니다.

---

Benchmarks

이 섹션에서는 고전적 MAPF 알고리즘들이 어떻게 평가되었는지, 이 목적을 위한 조직적인 벤치마크를 제안하고, 다른 관련 벤치마크 세트를 소개합니다.

4.1 Characteristics of a MAPF Benchmark

MAPF 문제는 그래프와 출발 및 목표 정점의 집합으로 정의됩니다. 따라서, MAPF를 위한 벤치마크는 여러 그래프와 각 그래프에 대한 출발 및 목표 정점 세트들을 포함합니다.

• Graphs for evaluating MAPF algorithms:
  
  • Dragon Age Origins (DAO) maps: 이것들은 게임 Dragon Age Origin에서 가져온 그리드들로, Sturtevant의 movingai.com 저장소에서 공개적으로 사용 가능합니다(Sturtevant 2012). 이 그리드들은 상대적으로 크고 개방적이며, 일부 그리드는 1000×1000 크기 이상입니다. 
  • Open N × N grids: 이것들은 N × N 그리드이며, 흔한 N 값은 8, 16, 32입니다. 이런 그리드는 에이전트의 밀도가 높은 실험을 가능하게 합니다.
  • N × N grids with random obstacles: 이것들은 N × N 그리드이며, 일부 그리드 셀이 임의로 선택되어 불가통과(장애물)로 간주됩니다(Standley 2010).
  • Warehouse grids: 실제 자율 창고 응용에서 영감을 받아, 최근 MAPF 논문들은 긴 복도가 있는 창고와 유사한 형태로 만들어진 그리드를 실험에 사용하고 있습니다(Ma et al. 2017; Cohen et al. 2018a). 그림 4는 창고 그리드의 예시를 보여줍니다(Cohen et al. 2018a).

4.2 Sources and targets assignments

지도 유형을 선택한 후, 에이전트의 출발지와 목적지 정점을 설정해야 합니다. 문헌에서 에이전트의 출발지 및 목적지를 설정하기 위해 사용된 여러 방법은 다음과 같습니다.

• Random: 임의로 정점을 선택하고 그래프 내에 경로가 있는지 확인하여 출발지와 목적지를 설정합니다.
• Clustered: 첫 번째 에이전트의 출발지와 목적지를 그래프 내에서 임의로 선택합니다. 모든 다른 에이전트의 출발지와 목적지를 첫 번째 에이전트의 출발지 및 목적지에서 최대 r 거리 내에 설정합니다.
• Designated: 각 에이전트의 출발지를 지정된 가능한 출발지 세트에서 임의로 선택하고, 각 에이전트의 목적지를 지정된 가능한 목적지 세트에서 유사하게 선택합니다.
  임의 할당은 문헌에서 가장 흔한 방법입니다. 군집화된 할당 방법은 MAPF 문제를 더 도전적으로 만들기 위해 사용되었습니다. 지정된 할당 방법은 자율 창고(Sturtevant et al. 2018) 및 교차로에서의 자율 차량(Švancara et al. 2019)을 시뮬레이션하기 위한 노력의 일환으로 이전 작업에서 사용되었습니다. 

4.3 Publicly Available MAPF Benchmarks

여기서는 MAPF 연구를 위한 두 가지 공개적으로 사용 가능한 벤치마크를 소개합니다.

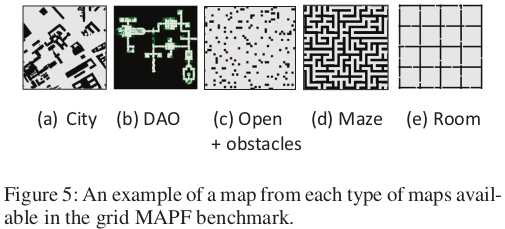
• Grid-based MAPF: 그리드 기반 MAPF 벤치마크는 24개의 맵으로 구성되며, 이는 (1) 실제 도시의 맵, (2) 비디오 게임 Dragon Age Origins와 Dragon Age 2, (3) 임의의 장애물이 있는 및 없는 열린 그리드, (4) 미로 같은 그리드, (5) 방 같은 그리드에서 가져온 것입니다. 모든 맵은 MovingAI 경로 찾기 저장소(Sturtevant 2012)에서 가져왔습니다. 각 맵에는 25개의 시나리오가 있으며, 각 시나리오는 임의 방식의 변형을 사용하여 설정된 출발지와 목적지 정점 목록을 가집니다. 각 맵의 가장 큰 도달 가능 지역의 모든 점들은 임의로 짝지어졌고, 그 후 첫 1000개의 문제가 시나리오에 포함되었습니다. 따라서, 출발지와 목적지 정점의 부분 집합을 선택하여 각 시나리오에서 MAPF 문제 세트를 생성할 수 있습니다.
  
  이 벤치마크를 사용하는 제안된 방법은 다음과 같습니다. 선택한 MAPF 알고리즘, 맵 유형 및 시나리오에 대해, 각 시나리오에서 가능한 한 많은 에이전트를 해결하려고 시도합니다. 즉, 선택한 시나리오와 관련된 처음 두 출발지-목적지 쌍을 사용하여 두 에이전트의 MAPF 문제를 생성하고 선택한 MAPF 알고리즘을 실행하여 이 문제를 해결합니다. 선택한 알고리즘이 이 MAPF 문제를 합리적인 시간 내에 성공적으로 해결하면, 그 시나리오의 처음 세 출발지-목적지 쌍을 사용하여 3 에이전트의 새로운 MAPF 문제를 생성하고 선택한 MAPF 알고리즘으로 해결하려고 시도합니다. 이 과정은 선택한 알고리즘이 생성된 MAPF 문제를 합리적인 시간 내에 해결할 수 없을 때까지 반복적으로 진행됩니다. 평가된 알고리즘은 그 후 각 시나리오에 대해 합리적인 시간 내에 해결할 수 있었던 최대 에이전트 수를 보고할 수 있습니다.
  
  비교를 위한 기준을 제공하기 위해, 우리는 이 평가 과정을 ICBS(Boyarski et al. 2015)를 사용하여 수행했습니다. 이 논문에서 도입된 용어를 사용하여, 우리의 설정은 4-이웃 그리드에서 고전적인 MAPF 설정이었으며, (1) 변, 정점 및 위치 교환 충돌이 금지되었고, (2) 따라가기 및 순환 충돌이 허용되었으며, (3) 목표는 비용의 합이었고, (4) 목표에서 에이전트의 행동은 목표에 머무르기였습니다.
  
  표 1은 이 평가의 결과를 보여줍니다. 실행 시간 제한으로 30초를 설정했습니다. 다른 행들은 다른 맵에 해당합니다. "크기" 열은 각 맵의 행과 열 수를 보고합니다. "문제" 열은 각 맵에 대해 사용 가능한 문제 수를 보고합니다. 이 숫자는 25개의 시나리오에 걸쳐 집계된 것으로, 시나리오에서 사용 가능한 문제 수는 해당 시나리오에 정의된
  
   출발지-목적지 쌍의 수입니다. "해결됨" 열은 지정된 시간 제한(30초) 내에 ICBS가 해결한 문제 수를 보고합니다. 보듯이 ICBS는 많은 문제를 해결할 수 있지만, 이 벤치마크의 문제들은 충분히 복잡하여 ICBS가 할당된 시간 내에 해결할 수 없는 많은 문제들이 있습니다. 따라서 이 그리드 MAPF 벤치마크의 문제들은 현대 MAPF 솔버들에게 도전이 될 만큼 어렵습니다.
  
  표 1에는 "최소"와 "최대"라는 두 개의 추가 열이 있습니다. 이 열들은 ICBS가 가장 적은 에이전트("최소")를 해결한 시나리오와 가장 많은 에이전트("최대")를 해결한 시나리오에서 해결한 최대 에이전트 수를 보고합니다. 예를 들어, brc202d 맵의 "최소" 값은 2이고 "최대" 값은 22입니다. 이는 ICBS가 타임아웃에 도달하기 전에 최대 2명의 에이전트만 해결할 수 있는 시나리오가 이 맵에 존재하며, 이 맵의 다른 시나리오에서는 ICBS가 최대 22명의 에이전트를 해결할 수 있었다는 것을 의미합니다. 이 값들은 동일한 맵의 시나리오 간 난이도의 다양성을 보여주기 위해 보고됩니다.

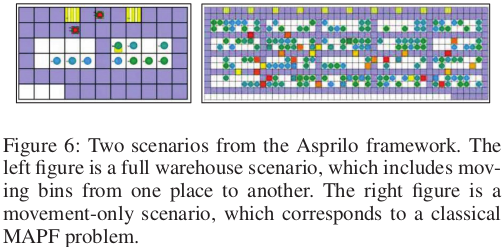
• Asprilo: MAPF 연구에 유용한 추가 도구는 Asprilo입니다. Asprilo는 자동화된 창고를 시뮬레이션하기 위한 공개적으로 사용 가능한 프레임워크입니다(Gebser et al. 2018). 이것은 표준 자동화된 창고 계획 문제를 정의하고 생성하기 위한 도구와 이러한 문제를 해결하는 계획을 검증하고 시각화하기 위한 도구를 포함합니다. Asprilo에서 지원하는 계획 문제 유형은 창고 내에서 한 곳에서 다른 곳으로 바구니를 옮기는 로봇에게 할당된 작업을 포함합니다. 그림 6은 Asprilo의 두 시나리오를 보여줍니다. 왼쪽에 있는 시나리오는 에이전트들이 한 곳에서 다른 곳으로 바구니를 옮기는 전체 창고 시나리오이며, 오른쪽은 이동만을 포함하는 시나리오, 즉 고전적 MAPF 문제입니다. Asprilo에 대한 자세한 내용은 (Gebser et al. 2018)과 프로젝트 웹사이트에서 확인할 수 있습니다.

 

---

5 Conclusion

이 논문의 첫 부분에서는 "고전적" 다중 에이전트 경로 찾기(MAPF) 문제에서 흔히 볼 수 있는 가정들을 정의하고 그들 사이의 관계를 논의했습니다. 그 후, 이전에 발표된 고전적 MAPF에 대한 주목할 만한 확장들을 정의했습니다. 논문의 두 번째 부분에서는 새로운 MAPF 벤치마크 문제 모음을 소개하고 다른 MAPF 벤치마크 문제 세트를 지적했습니다. 이 논문의 두 부분 모두 MAPF 연구를 위한 공통 언어, 용어 및 실험 설정을 제안하기 위한 것입니다. 우리는 향후 MAPF 연구자들이 우리의 용어를 따르고 이 벤치마크들을 유용하게 사용할 것이라고 희망합니다.