Abstract 정리
멀티 에이전트 경로 찾기(MAPF)는 에이전트 팀을 충돌 없이 목표 위치로 이동시키는 문제입니다. 이 논문에서는 대규모 자동화된 창고와 같이, 에이전트들이 새로운 목표 위치에 지속적으로 참여하는 lifelong MAPF의 변형을 연구합니다. 우리는 decompose
the problem into a sequence of Windowed MAPF instances하는 lifelong MAPF를 해결하기 위한 새로운 프레임워크인 Rolling-Horizon Collision Resolution(RHCR)을 제안합니다. 여기서 Windowed MAPF 솔버는 bounded time horizon 내에서만 에이전트들의 경로 간 충돌을 해결하고 그 너머의 충돌은 무시 (가정)합니다. RHCR은 지속적으로 도착하는 새로운 목표 위치에 적응하는 유연한 계획을 생성하는 데 특히 적합 (이 논문의 장점)합니다. 우리는 다양한 MAPF 솔버와 함께 RHCR을 실증적으로 평가하고, 이를 통해 최대 1,000명의 에이전트(지도상 빈 셀의 38.9%)에 대해 고품질의 해결책을 생산할 수 있으며, 이는 기존 작업을 크게 능가한다는 것을 보여줍니다.
Introduction 정리
멀티 에이전트 경로 찾기(MAPF)는 에이전트 팀을 시작 위치에서 목표 위치로 이동시키면서 충돌을 피하는 문제입니다. 솔루션의 품질은 flowtime(모든 에이전트가 목표 위치에 도착하는 시간의 합) 또는 makespan(모든 에이전트가 목표 위치에 도착하는 시간 중 최대값)으로 측정됩니다. MAPF는 최적으로 해결하기 NP-하드 문제입니다(Yu and LaValle 2013).
MAPF는 자율 항공기 견인 차량(Morris et al. 2016), 비디오 게임 캐릭터(Li et al. 2020b), 쿼드로터 무리(Hönig et al. 2018) 등과 같은 다양한 실제 응용 분야가 있습니다. 현재, 자동화된 창고에서는 드라이브 유닛이라고 불리는 모바일 로봇들이 자율적으로 인벤토리 포드나 평평한 패키지를 한 위치에서 다른 위치로 이동시키고 있습니다(Wurman, D'Andrea, and Mountz 2007; Kou et al. 2020). 그러나, 많은 응용 분야에서 실제 문제는 "one-shot" MAPF 변형일 뿐입니다. (기존 방법론의 한계점) 일반적으로 에이전트가 목표 위치에 도달한 후에는 영원히 거기에서 멈추고 기다리지 않습니다. 대신, 새로운 목표 위치가 할당되고 계속 이동해야 합니다. 이를 lifelong MAPF(Ma et al. 2017)라고 하며, 에이전트들이 지속적으로 새로운 목표 위치를 할당받는 것이 특징 (이 논문의 기여점)입니다.
기존의 lifelong MAPF 해결 방법에는
- 전체를 해결하는 방법(Nguyen et al. 2017)
- 모든 시간 단계에서 모든 에이전트에 대해 경로를 재계획하는 MAPF 인스턴스 시퀀스로 분해하는 방법(Wan et al. 2018; Grenouilleau, van Hoeve, and Hooker 2019)
- 새로운 목표 위치를 가진 에이전트에 대해서만 매 시간 단계에서 새로운 경로를 계획하는 MAPF 인스턴스 시퀀스로 분해하는 방법(Cáp, Vokrı́nek, and Kleiner 2015; Ma et al. 2017; Liu et al. 2019)이 있습니다.
이 논문에서는 lifelong MAPF를 windowed MAPF 인스턴스의 시퀀스로 분해하고 매 h 시간 단계마다(사용자가 지정한 재계획 기간 h) 계획과 실행을 교차하면서 경로를 재계획하는 새로운 프레임워크인 롤링-호라이즌 충돌 해결(RHCR)을 제안합니다. (we propose a new framework Rolling-Horizon Collision Resolution (RHCR) for solving lifelong MAPF where we decompose lifelong MAPF into a sequence of Windowed MAPF instances and replan paths once every h timesteps (replanning period h is user-specified) for interleaving planning and execution.) Windowed MAPF 인스턴스는 다음과 같은 방식으로 일반 MAPF 인스턴스와 다릅니다:
- 에이전트에게 동일한 windowed MAPF 에피소드 내에서 일련의 목표 위치가 할당될 수 있으며,
- 첫 번째 w 시간 단계(사용자가 지정한 시간 지평선 w ≥ h)에 대해서만 충돌을 해결해야 합니다.
이 분해의 이점은 두 가지입니다. 첫째, 에이전트를 지속적으로 활동시켜 유휴 시간을 피하고 처리량을 늘립니다. 둘째, 지속적으로 도착하는 새로운 목표 위치에 적응하는 유연한 계획을 생성합니다. 사실, 전체 시간 지평선에서 충돌을 해결하는 것(w = ∞)은 종종 불필요합니다. 새로운 목표 위치가 도착함에 따라 에이전트의 경로가 변경될 수 있기 때문입니다.
우리는 RHCR을 다양한 MAPF 솔버인 CA*(Silver 2005) (완전하지 않고 최적화되지 않음), PBS (Ma et al. 2019) (완전하지 않고 최적화되지 않음), ECBS (Barer et al. 2014) (완전하고 최적화되지 않음), CBS (Sharon et al. 2015) (완전하고 최적화됨)와 함께 평가합니다. 우리는 각 MAPF 솔버에 대해 bounded time horizon을 사용하면 전체 시간 지평선을 사용하는 것과 유사한 처리량을 얻을 수 있지만 실행 시간이 훨씬 적다 (bounded time horizon 를 사용하는 이점)는 것을 보여줍니다. 또한 RHCR이 기존 작업을 능가하고 시뮬레이션된 창고 인스턴스에 대해 최대 1,000명의 에이전트(지도상 빈 셀의 38.9%)까지 확장할 수 있다는 것을 보여줍니다.
Background
이 섹션에서는 먼저 최신 MAPF(Multi-Agent Path Finding) 솔버들을 소개한 다음, 평생 MAPF에 대한 기존 연구를 논의합니다. 마지막으로, 이전 연구를 안내한 유한 시간 지평선 아이디어의 요소들을 검토합니다.
2.1 Popular MAPF Solvers
최근 몇 년 동안 많은 MAPF 솔버들이 제안되었습니다. 여기에는 규칙 기반 솔버(Luna and Bekris 2011; de Wilde, ter Mors, and Witteveen 2013), 우선 순위 계획(Okumura et al. 2019), 컴파일 기반 솔버(Lam et al. 2019; Surynek 2019), A*-기반 솔버(Goldenberg et al. 2014; Wagner 2015), dedicated search-based solvers(Sharon et al. 2013; Barer et al. 2014)가 포함됩니다. 우리는 네 가지 대표적인 MAPF 솔버를 소개합니다.
CBS(Conflict-Based Search)는 완전하고 최적인 인기 있는 2단계 MAPF 솔버입니다(Sharon et al. 2015). 상위 수준에서 CBS는 각 에이전트를 위한 최단 경로를 포함하는 루트 노드로 시작합니다(다른 에이전트를 무시). 그런 다음 충돌을 선택하여 해결하기 위해 두 개의 자식 노드를 생성하고, 각 노드에 충돌 위치에서 충돌 시간에 있는 에이전트 중 하나가 있을 수 없도록 하는 추가적인 제약 조건을 추가합니다. 그런 다음 새로운 제약 조건으로 에이전트의 경로를 재계획하기 위해 하위 수준을 호출합니다. CBS는 충돌이 없는 경로가 있는 노드를 찾을 때까지 이 절차를 반복합니다. CBS와 그 향상된 변형들(Gange, Harabor, and Stuckey 2019; Li et al. 2019, 2020a)은 최신 최적 MAPF 솔버들 중 하나입니다. (완전하고 최적화됨)
ECBS(Enhanced CBS)는 CBS의 완전하고 경계-부분 최적 변형입니다(Barer et al. 2014). 경계 부분 최적성(즉, 솔루션 비용이 사용자 지정 요인만큼 최적 비용에서 벗어남)은 CBS의 고위 및 저위 수준 검색 모두에서 최선의 검색 대신 포컬 검색(Pearl and Kim 1982)을 사용함으로써 달성됩니다. ECBS는 최신 경계-부분 최적 MAPF 솔버입니다. (완전하고 최적화되지 않음),
CA*(Cooperative A*)는 간단한 우선 순위 계획 방식을 기반으로 합니다(Silver 2005). 각 에이전트는 고유한 우선 순위를 부여받고, 우선 순위 순으로 더 높은 우선 순위를 가진 에이전트의 (이미 계획된) 경로와 충돌하지 않는 최단 경로를 계산합니다. CA* 또는 일반적으로 우선 순위 계획은 실행 시간이 짧기 때문에 실제로 널리 사용됩니다. 그러나 사전에 정의된 우선 순위 순서로 인해 때때로 해결 가능한 MAPF 인스턴스에 대한 해결책의 품질이 나쁘거나 해결책을 찾지 못할 수 있으므로 부분 최적이며 불완전 (단점)합니다. (완전하지 않고 최적화되지 않음),
PBS(Priority-Based Search)는 CBS와 CA*의 아이디어를 결합합니다(Ma et al. 2019). PBS의 상위 수준은 CBS와 유사하지만, 충돌을 해결할 때 자식 노드에 추가적인 제약 조건을 추가하는 대신, 충돌에 관련된 에이전트 중 하나에게 다른 에이전트보다 높은 우선 순위를 부여합니다. PBS의 하위 수준은 상위 수준에서 생성된 부분 우선 순위 순서와 일치하는 최단 경로를 계획하는 CA*와 유사합니다. PBS는 솔루션 품질 측면에서 많은 우선 순위 계획 변형을 능가하지만 여전히 불완전하고 부분 최적입니다. (완전하지 않고 최적화되지 않음)
2.2 Prior Work on Lifelong MAPF
Lifelong MAPF에 대한 기존 연구를 세 가지 범주로 분류합니다.

Method (1) 첫 번째 방법은 평생 MAPF를 오프라인 설정(즉, 모든 목표 위치를 사전에 알고 있음)에서 전체적으로 해결하는 것입니다. 이는 평생 MAPF를 다른 잘 연구된 문제로 환원합니다. 예를 들어, Nguyen et al. (2017)은 평생 MAPF를 답변 집합 프로그래밍 문제로 공식화했습니다. 그러나 이 방법은 그들의 논문에서 20명의 에이전트에 대해서만 확장되며, 각각은 약 4개의 목표 위치만 가집니다. 이는 MAPF가 어려운 문제이고 그 평생 변형은 더 어렵기 때문에 놀라운 일이 아닙니다.
Method (2) 두 번째 방법은 평생 MAPF를 일련의 MAPF 인스턴스로 분해하고, 매 타임스텝마다 모든 에이전트에 대한 경로를 재계획하는 것입니다. 확장성을 개선하기 위해, 연구자들은 이전 검색 노력을 재사용하는 점진적 검색 기술을 개발했습니다. 예를 들어, Wan et al. (2018)은 이전 고위 수준 검색의 트리를 재사용하는 CBS의 점진적 변형을 제안했습니다. 그러나 이전 트리에서 새로운 고위 트리를 구축하는 데 상당한 오버헤드가 있어 확장성을 크게 개선하지 못합니다. Svancara et al. (2019)은 이전 반복에서 경로를 재사용하기 위해 독립성 탐지(Standley 2010) 프레임워크를 사용합니다. 이는 새로운 에이전트(본 경우, 새로운 목표 위치를 가진 에이전트)와 새로운 에이전트의 경로에 영향을 받는 에이전트의 경로만 재계획합니다. 그러나 환경이 밀집되어 있을 때(즉, 많은 에이전트와 장애물이 있는 것이 창고 시나리오에서 일반적), 거의 모든 경로가 영향을 받으므로 대부분의 에이전트에 대한 경로를 재계획해야 합니다.
Method (3) 세 번째 방법은 두 번째 방법과 유사하지만, 목표 위치에 도달한 에이전트의 경로만 재계획하는 것에 제한을 둡니다. 새로운 경로는 서로뿐만 아니라 다른 에이전트의 경로와 충돌을 피해야 합니다. 따라서, 이 방법은 매 타임스텝마다 하나의 에이전트만 목표 위치에 도달하는 경우 우선 순위 계획으로 퇴화될 수 있습니다. 결과적으로, 우선 순위 계획의 일반적인 단점인 불완전성과 비용이 많이 드는 솔루션 생성 가능성이 이 방법에서 다시 나타납니다. 불완전성 문제를 해결하기 위해 Cáp, Vokrı́nek, and Kleiner (2015)는 되돌리기 없는 검색 (backtrack-free search)을 가능하게 하는 잘 형성된 인프라의 아이디어를 도입합니다. 잘 형성된 인프라에서는 모든 가능한 목표 위치가 엔드포인트로 간주되며, 모든 엔드포인트 쌍에 대해 다른 엔드포인트를 통과하지 않고 연결하는 경로가 존재합니다. 실제 응용에서, 일부 지도(예: 그림 1a에서와 같이)는 이 요구 사항을 충족할 수 있지만, 다른 지도(예: 그림 1b에서와 같이)는 그렇지 않을 수 있습니다. 또한, 경로 계획 중 추가 메커니즘이 필요합니다. 예를 들어, 에이전트가 목표 위치를 "유지"하도록 강제하거나(Ma et al. 2017) 에이전트에 대한 "더미 경로"(Liu et al. 2019)를 계획해야 합니다. 두 대안 모두 불필요하게 긴 경로를 에이전트에게 제공하여, 우리의 실험에서 보여진 것처럼 전체 처리량을 감소시킵니다.
Summary 방법 (1)은 모든 목표 위치를 사전에 알아야 하며 확장성이 제한적입니다. 방법 (2)는 온라인 설정에서 작동할 수 있으며 방법 (1)보다 더 잘 확장됩니다. 그러나 점진적 검색 기술을 사용하더라도 매 타임스텝마다 모든 에이전트에 대한 재계획은 시간이 많이 걸립니다. 결과적으로 확장성도 제한적입니다. 방법 (3)은 처음 두 방법보다 훨씬 더 많은 에이전트에 확장할 수 있지만, 완전성을 보장하기 위해 지도에 추가적인 구조가 있어야 합니다. 결과적으로, 특정 클래스의 평생 MAPF 인스턴스에만 작동합니다. 또한, 방법 (2)와 (3)은 매 타임스텝에서 계획하는데, 계획이 시간이 많이 걸리므로 실용적이지 않을 수 있습니다.
2.3 Bounded-Horizon Planing
Bounded-horizon planning은 새로운 아이디어가 아닙니다. Silver (2005)는 이미 일반 MAPF에 CA*로 이 아이디어를 적용했습니다. 그는 이를 Windowed Hierarchical Cooperative A*(WHCA*)라고 부르며, WHCA*가 유한 bounded horizon의 길이가 줄어들수록 더 빨리 실행되지만 더 긴 경로를 생성한다는 것을 실증적으로 보여줍니다. 이 논문에서는 longlife MAPF 및 다른 MAPF 솔버에 이 아이디어를 적용하는 이점을 보여줍니다. 특히, RHCR은 유한 시간 지평선으로 계획할 때 낮은 계산 비용의 이점을 제공하면서도 에이전트를 바쁘게 유지하고, 일반 MAPF에 대한 WHCA*와 달리 솔루션 품질을 약간만 감소시킵니다.
3 Problem Definition
입력은 위치 V에 해당하는 정점과 두 인접 위치 사이의 연결을 나타내는 간선 E를 가진 그래프 \(G = (V, E)\)와 초기 위치가 있는 \(m\)명의 에이전트 \(\{a_1, \ldots, a_m\}\) 집합입니다. 우리는 모든 목표 위치를 사전에 알지 못하는 온라인 설정을 연구합니다. 경로 계획 시스템 외부에 있는 작업 할당자가 있다고 가정하며, 에이전트들은 시스템 운영 중에 작업 할당자에게 목표 위치를 요청할 수 있습니다. 시간은 타임스텝으로 이산화됩니다. 각 타임스텝에서, 모든 에이전트는 인접 위치로 이동하거나 현재 위치에서 대기할 수 있습니다. 이동 및 대기 행동 모두 단위 기간을 가집니다. 충돌은 두 에이전트가 동일한 타임스텝에 같은 위치를 차지하거나(Stern et al. 2019에서 언급된 정점 충돌) 동일한 타임스텝에 같은 간선을 반대 방향으로 통과하는 경우에 발생합니다(Stern et al. 2019에서 언급된 위치 교환 충돌). 우리의 임무는 모든 에이전트를 그들의 목표 위치로 이동시키고 처리량, 즉 타임스텝당 평균 방문 목표 위치 수를 최대화하는 충돌 없는 경로를 계획하는 것입니다. 모든 에이전트에 대한 충돌 없는 경로 세트를 MAPF 계획이라고 합니다.
우리는 작업 할당자가 우리의 제어 범위에 있지 않은 경우를 연구하여, 다양한 도메인에서 우리의 경로 계획 시스템을 적용할 수 있도록 합니다. 그러나 특정 도메인의 경우, 도메인 특정 작업 할당자와 도메인 독립적 경로 계획 시스템을 결합하는 계층적 프레임워크를 설계할 수 있습니다. 작업 할당 및 경로 찾기를 함께 해결하는 결합 방법과 비교하여, 계층적 프레임워크는 일반적으로 효율성을 달성하는 좋은 방법입니다. 예를 들어, 충족 창고 응용 프로그램(Ma et al. 2017; Liu et al. 2019) 및 분류 센터 응용 프로그램(Grenouilleau, van Hoeve, and Hooker 2019)에 대한 작업 할당자는 우리의 경로 계획 시스템과 직접 결합될 수 있습니다. 우리는 또한 각 응용 프로그램에 대해 하나씩 두 가지 간단한 작업 할당자를 실험에서 보여줍니다.
우리는 드라이브 유닛이 어떤 MAPF 계획이든 완벽하게 실행할 수 있다고 가정합니다. 비현실적으로 보일 수 있지만, 드라이브 유닛의 운동학적 제약을 고려하고 MAPF 계획을 견고한 실행을 위한 실행 가능한 명령으로 변환할 수 있는 일부 사후 처리 방법이 있습니다. 예를 들어, Hönig et al. (2019)은 계획과 실행을 교차하는 프레임워크를 제안하고 이를 우리 프레임워크 RHCR과 직접 결합할 수 있습니다.
4 Rolling-Horizon Collision Resolution
롤링-호라이즌 충돌 해결(RHCR)은 두 가지 사용자 지정 매개변수, 즉 time horizon \(w\)와 replanning period \(h\)를 가집니다. 시간 지평선 \(w\)는 윈도우드 MAPF 솔버가 \(w\) 타임스텝의 시간 지평선 내에서 충돌을 해결해야 함을 명시합니다. 재계획 기간 \(h\)는 윈도우드 MAPF 솔버가 매 \(h\) 타임스텝마다 경로를 재계획해야 함을 명시합니다. 윈도우드 MAPF 솔버는 충돌을 피하기 위해 \(w\) 타임스텝보다 더 자주 경로를 재계획해야 합니다. 즉, \(w\)는 \(h\)보다 크거나 같아야 합니다.
매 윈도우드 MAPF 에피소드에서, 예를 들어 \(t\) 타임스텝에서 시작할 때, RHCR은 먼저 각 에이전트 \(a_i\)에 대한 시작 위치 \(s_i\)와 목표 위치 순서 \(g_i\)를 업데이트합니다. RHCR은 에이전트 \(a_i\)의 시작 위치 \(s_i\)를 \(t\) 타임스텝에서의 위치로 설정합니다. 그런 다음, RHCR은 에이전트 \(a_i\)가 \(g_i\)에 남아 있는 모든 위치를 방문하는 데 필요한 타임스텝의 하한 \(d\)를 계산합니다.
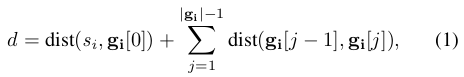
여기서 \(dist(x, y)\)는 위치 \(x\)에서 위치 \(y\)까지의 거리이고 \(|x|\)는 순서 \(x\)의 cardinality입니다. \(d\)가 \(h\)보다 작다는 것은 에이전트 \(a_i\)가 다음 윈도우드 MAPF 에피소드가 \(t + h\) 타임스텝에서 시작하기 전에 모든 목표 위치를 방문하고 나서 유휴 상태가 될 수 있음을 나타냅니다. 이 상황을 피하기 위해, RHCR은 \(d ≥ h\)가 될 때까지 지속적으로 에이전트 \(a_i\)에게 새로운 목표 위치를 할당합니다. 모든 에이전트의 시작 위치와 목표 위치 순서에 더 이상 업데이트가 필요 없게 되면, RHCR은 윈도우드 MAPF 솔버를 호출 (RHCR에서 MAPF 솔버로 변경; 몇몇 에이전트만 업데이트가 필요없으면 어떻게 되는거지? 더이상 없데이트가 불필요한 agent들의 goal을 현재위치로 하면 가능할 수도?)하여 모든 에이전트가 충돌 없이 첫 \(w\) 타임스텝 동안 이동하고, 그들의 목표 위치 순서에 주어진 순서대로 모든 목표 위치로 이동하는 경로를 찾습니다. 마지막으로, 생성된 경로를 따라 \(h\) 타임스텝 동안 에이전트를 이동시키고 그들의 목표 위치 순서에서 방문한 목표 위치를 제거합니다.
RHCR은 윈도우드 MAPF 솔버의 목표로 플로우타임을 사용하는데, 이는 평생 MAPF에 대해 합리적인 목표로 알려져 있습니다(Svancara et al. 2019). 일반적인 MAPF 솔버와 비교하여, 윈도우드 MAPF 솔버는 두 가지 측면에서 변경이 필요합니다.
1. 각 경로는 일련의 목표 위치를 방문해야 하며,
2. 경로는 첫 \(w\) 타임스텝 동안만 충돌 없이 이동해야 합니다.
다음 두 하위 섹션에서 이러한 변경 사항을 자세히 설명합니다.
4.1 A* for a Goal Location Sequence

2.1절에서 논의된 모든 MAPF 솔버의 저수준 검색은 에이전트가 시작 위치에서 목표 위치로 이동하는 경로를 찾아야 하며, 특정 시간 단계에서 특정 위치에 있지 않도록 하는 공간-시간 제약 조건을 만족시켜야 합니다. 따라서, 이들은 종종 location-time A*(Silver 2005) (즉, 각 상태가 위치와 타임스텝의 쌍인 location-time space에서 검색하는 A*) 또는 그 변형 중 하나를 사용합니다. 그러나 윈도우드 MAPF 솔버의 특징적인 기능은 각 에이전트에 대해 sequence of goal locations를 방문하는 경로를 계획한다는 것입니다. 이 차이에도 불구하고, 일반 MAPF 솔버의 저수준 검색에서 사용되는 기술은 윈도우드 MAPF 솔버의 저수준 검색에 적응될 수 있습니다. 사실, Grenouilleau, van Hoeve, and Hooker (2019)는 이러한 적응의 단축 버전을 픽업 및 배송 문제에 적용합니다. 그들은 단일 에이전트가 할당된 픽업 위치와 목표 위치라는 두 개의 순서대로 정렬된 목표 위치를 방문하는 경로를 찾을 수 있는 멀티 레이블 A*를 제안합니다. 알고리즘 1에서는 멀티 레이블 A*를 일련의 목표 위치에 일반화합니다. (에이전트가 일련의 목표 위치를 방문하기 위한 경로를 계획하는 것은 간단하지 않습니다. 연속적인 목표 위치 사이에 가장 짧은 경로를 계획하기 위해 위치-시간 A*의 시퀀스를 호출하고 결과 경로를 연결할 수 있지만, 공간-시간 제약이 다른 목표 위치 간 경로 부분에 공간-시간 의존성을 도입하기 때문에 전체 경로가 반드시 가장 짧은 것은 아닙니다. 예를 들어, 첫 번째 목표 위치에 가능한 가장 빠른 타임스텝에 도착하는 것이 나중에 도착하는 것보다 전체 경로가 더 길어질 수 있습니다. 따라서 알고리즘 1이 필요합니다. <= 공간-시간 제약 때문에 전체 경로가 항상 짧지 않을 수 있다. 알고리즘 1이 이 문제를 해결하는데 어떻게? 아마도 15행의 dist cost가 뒤쪽의 goal까지의 거리를 포함하고 있어서 전체 경로가 짧은걸 가능하게 만든다는 걸로 판단됨.)
알고리즘 1은 위치-시간 A*의 구조를 사용합니다. 각 노드 \(N\)에 대해 추가 속성 \(N.label\)을 추가하여 목표 위치 순서 \(g_i\)의 목표 위치 수를 루트 노드에서 노드 \(N\)까지의 경로가 이미 방문한 것을 나타냅니다. 예를 들어, \(N.label = 2\)는 경로가 이미 목표 위치 \(g_i[0]\)과 \(g_i[1]\)을 방문했지만 목표 위치 \(g_i[2]\)는 방문하지 않았음을 나타냅니다. 알고리즘 1은 노드의 \(h\)-값을 노드의 위치에서 다음 목표 위치까지의 거리와 목표 위치 순서의 연속적인 미래 목표 위치 간 거리의 합으로 계산합니다[14-15행]. 주요 절차에서, 알고리즘 1은 먼저 레이블 0을 가진 루트 노드 \(R\)을 생성하고 우선 순위 큐 open에 푸시합니다[1-4행]. open이 비어 있지 않은 동안[5행], \(f\)-값이 가장 작은 노드 \(P\)가 확장을 위해 선택됩니다[6행]. \(P\)가 현재 목표 위치에 도달했다면[7행], \(P.label\)은 증가됩니다[8행]. \(P.label\)이 목표 위치 순서의 기수와 같다면[9행], 알고리즘 1은 종료하고 경로를 반환합니다[10행]. 그렇지 않으면, 주어진 공간-시간 제약 조건을 존중하는 자식 노드들을 생성합니다[11-12행]. 자식 노드의 레이블은 \(P.label\)과 같습니다. 우선 순위 큐에서 중복을 확인하려면 다른 속성 외에 레이블 비교가 필요합니다. (알고리즘 1 설명: 각 agent i는 $|g_i|$ 갯수의 goal을 가지고 있고 각 goal은 $g_i[P.label]$ 이다. 따라서, 각 label에 따른 $A^{*}$를 수행하여 각 goal에 도달하는 path를 생성한다.)
4.2 Bounded-Horizon MAPF Solvers
윈도우드 MAPF 솔버의 또 다른 특징적인 기능은 유한 시간 지평선의 사용입니다. 일반적인 MAPF 솔버는 첫 번째 \(w\) 타임스텝 동안의 충돌만 해결하도록 쉽게 적응될 수 있습니다. 첫 번째 \(w\) 타임스텝 이후에는 솔버가 에이전트들 간의 충돌을 무시하고 각 에이전트가 모든 목표 위치를 방문하기 위해 최단 경로를 따른다고 가정합니다. 이는 대부분의 경우에 에이전트들이 올바른 방향으로 이동하도록 보장합니다. 이제 2.1절에서 논의된 다양한 MAPF 솔버를 수정하는 방법에 대한 세부 정보를 제공합니다. ($w$ 타임스텝을 각 solver에 어떻게 적용하는지에 대한 내용; 간단하게 요약하면 단순히 $w$ 시간동안만 해당 solver 알고리즘을 쓰고 나머지 시간은 무시한다는 내용)
Bounded-Horizon (E)CBS
CBS와 ECBS는 충돌을 탐지하고 해결함으로써 검색합니다. 유한 시간 지평선 변형에서는 충돌 탐지 기능만 수정하면 됩니다. (E)CBS는 모든 경로 간의 충돌을 찾고 그 중 하나를 해결할 수 있는 반면, 유한 시간 지평선 (E)CBS는 첫 번째 \(w\) 타임스텝에서 발생하는 모든 경로 간의 충돌만 찾아 그 중 하나를 해결할 수 있습니다. (E)CBS의 나머지 부분은 동일하게 유지됩니다. 유한 시간 지평선 (E)CBS는 더 적은 충돌을 해결해야 하므로 더 작은 고위 수준 트리를 생성하고 표준 (E)CBS보다 더 빠르게 실행됩니다.
Bounded-Horizon CA*
CA*는 우선 순위에 기반한 검색으로, 한 에이전트는 모든 높은 우선 순위를 가진 에이전트들과의 충돌을 피합니다. 유한 시간 지평선 변형에서는 에이전트가 첫 번째 \(w\) 타임스텝 동안만 더 높은 우선 순위를 가진 에이전트들과의 충돌을 피해야 합니다. 따라서 각 에이전트에 대해 위치-시간 A*를 실행할 때 첫 번째 \(w\) 타임스텝에서 더 높은 우선 순위를 가진 에이전트의 경로에 의해 유도되는 공간-시간 제약만 고려합니다. CA*의 나머지 부분은 동일하게 유지됩니다. 유한 시간 지평선 CA*는 더 적은 공간-시간 제약을 가지므로 CA*보다 더 빠르게 실행되며 솔루션을 찾지 못할 가능성이 적습니다. 유한 시간 지평선 CA*는 (Silver 2005)의 WHCA*와 동일합니다.
Bounded-Horizon PBS
PBS의 고위 수준 검색은 CBS와 유사하며 충돌을 해결하는 데 기반합니다. 반면 PBS의 저위 수준 검색은 CA*와 유사하며 고위 수준 검색에 의해 생성된 부분 우선 순위 순서와 일관된 경로를 계획합니다. 따라서 PBS의 고위 수준 충돌 탐지 기능을 수정해야 합니다(CBS 수정과 같이) 및 저위 수준의 제한된 공간-시간 제약을 통합해야 합니다(CA* 수정과 같이). 결과적으로, 유한 시간 지평선 PBS는 표준 PBS보다 작은 고위 수준 트리를 생성하고 저위 수준에서 더 빠르게 실행됩니다.
4.3 Behavior of RHCR
우리는 평생 MAPF에서 더 긴 시간 지평선에 대한 충돌을 해결하는 것이 반드시 더 나은 솔루션을 가져오는 것은 아니라는 것을 먼저 보여줍니다. 아래는 그러한 예입니다.
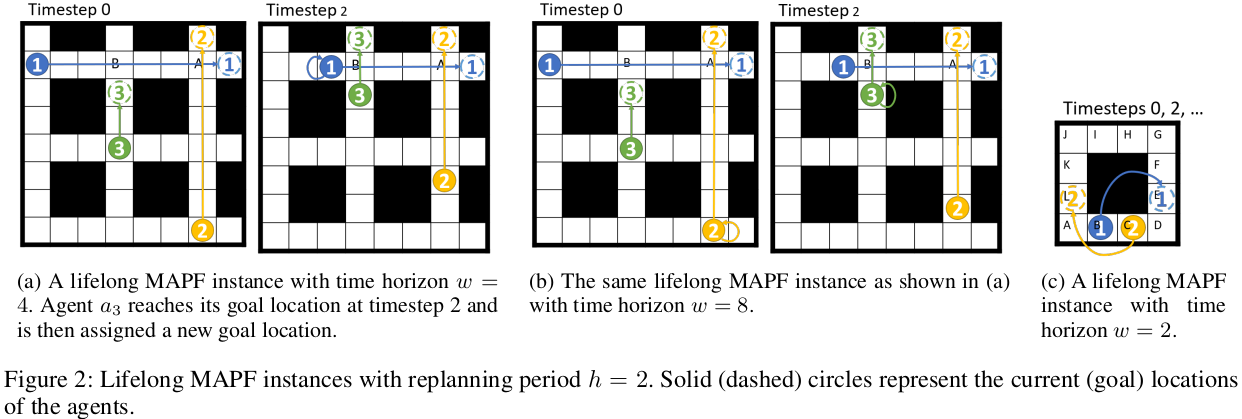
Example 1 (Figure 2.a,b; 짧은 time horizon의 효율성).
시간 지평선 \(w = 4\)와 재계획 기간 \(h = 2\)를 가진 그림 2a의 평생 MAPF 인스턴스를 고려하고, 최적의 윈도우드 MAPF 솔버를 사용한다고 가정합니다. 타임스텝 0(왼쪽 그림)에서 모든 에이전트는 첫 4 타임스텝 동안 충돌이 발생하지 않기 때문에 최단 경로를 따릅니다. 그런 다음 에이전트 \(a_3\)는 타임스텝 2에 목표 위치에 도달하고 새로운 목표 위치가 할당됩니다(오른쪽 그림). 에이전트 \(a_1\)과 \(a_3\)이 모두 최단 경로를 따른다면, 윈도우드 MAPF 솔버는 타임스텝 3의 셀 B에서 그들 사이의 충돌을 발견하고 에이전트 \(a_1\)에게 한 타임스텝 대기하도록 강제합니다. 결과적으로 대기 행동의 수는 1입니다. 그러나 시간 지평선 \(w = 8\)로 이 예제를 해결한다면, 그림 2b에서 보여지는 것처럼 더 많은 대기 행동이 있는 경로를 생성할 수 있습니다. 타임스텝 0(왼쪽 그림)에서 윈도우드 MAPF 솔버는 타임스텝 6의 셀 A에서 에이전트 \(a_1\)과 \(a_2\) 사이의 충돌을 발견하고 에이전트 \(a_2\)에게 한 타임스텝 대기하도록 강제합니다. 그런 다음 타임스텝 2(오른쪽 그림)에서 윈도우드 MAPF 솔버는 타임스텝 3의 셀 B에서 에이전트 \(a_1\)과 \(a_3\) 사이의 충돌을 발견하고 에이전트 \(a_3\)에게 한 타임스텝 대기하도록 강제합니다. 결과적으로 대기 행동의 수는 2입니다. (Figure2.a의 경우 w=4이고 $a_4$의 목적지도 짧기 때문에 timestep 0에서는 충돌이 안나다가 timestep2에서 $a_3$이 새로운 목적지를 얻으면서 충돌 가능성이 생기고 그래서 $a_1$이 1 step 기다리게 된다. 반면 Figure2.b의 경우 w=8이어서 처음부터 $a_2$와 $a_1$의 충돌을 감지하여 $a_2$가 1 step 기다리고 timestep 2에서 $a_1$과 $a_3$의 충돌을 또 감지하여 1 step을 기다리게 된다. 즉, w가 더 큰데 오히려 더 비효율적으로 움직이게 된다.)
우리의 실험에서도 유사한 경우가 발견되었습니다: 때때로 RHCR은 더 작은 시간 지평선으로 더 큰 시간 지평선보다 더 높은 처리량을 달성합니다. 이 모든 경우들은 평생 MAPF에서 전체 시간 지평선의 모든 충돌을 해결할 필요가 없다는 우리의 주장을 뒷받침합니다. 이는 일반 MAPF와 다릅니다. 그러나 유한 시간 지평선 방법은 너무 작은 시간 지평선 값을 사용하면 에이전트가 목표 위치에 도달하지 못하는 교착 상태를 생성할 수 있다는 단점도 있습니다. 예제 2에서 보여지듯이.
Example 2 (Figure 2.c; Deadlock 예제).
시간 지평선 \(w = 2\)와 재계획 기간 \(h = 2\)를 가진 그림 2c의 평생 MAPF 인스턴스를 고려하고, 최적의 윈도우드 MAPF 솔버를 사용한다고 가정합니다. 타임스텝 0에서 윈도우드 MAPF 솔버는 에이전트 \(a_1\)에게 길이 5인 경로 [B, B, B, C, D, E]와 에이전트 \(a_2\)에게 길이 5인 경로 [C, C, C, B, A, L]을 반환합니다. (왜 timestep 2까지 기다리는 경로가 나오는지 이해 안감.) 이는 첫 2 타임스텝 동안 충돌이 없습니다. 상단 복도를 사용하는 충돌 없는 경로나 하단 복도를 먼저 빠져나가 다른 에이전트가 목표 위치에 도달하도록 하고 다시 들어가는 충돌 없는 경로는 반환되지 않습니다. 그 결과의 플로우타임이 5 + 5 = 10보다 크기 때문입니다. 따라서 타임스텝 2에서 두 에이전트 모두 B와 C 셀에서 계속 기다리고 있습니다. 그런 다음 윈도우드 MAPF 솔버는 두 에이전트에 대해 같은 경로를 다시 찾고 그들을 두 타임스텝 더 기다리게 합니다. 전반적으로 에이전트들은 B와 C 셀에서 영원히 기다리고 결코 목표 위치에 도달하지 못합니다. ($a_1$와 $a_2$ 가 경로를 돌아가기에는 cost가 너무 크기때문에 서로를 통과하는 경로가 만들어지고 결국 deadlock이 생김.)
4.4 Avoiding Deadlocks
예제 2에서 보여진 교착 상태 문제를 해결하기 위해, 에이전트의 진행 상황을 평가하는 잠재적 함수를 설계하고 에이전트가 충분한 진행을 하지 못할 경우 시간 지평선을 늘릴 수 있습니다. 예를 들어, 윈도우드 MAPF 솔버가 경로 집합을 반환한 후, 잠재적 함수 \(P(w) = | \{ a_i | \text{COMPUTE HVALUE}(x_i, l_i) < \text{COMPUTE HVALUE}(s_i, 0), 1 \leq i \leq m \} |\)를 계산합니다. 여기서 함수 \(\text{COMPUTE HVALUE}(·, ·)\)는 알고리즘 1의 14-15번 줄에 정의되어 있으며, \(x_i\)는 타임스텝 \(w\)에서 에이전트 \(a_i\)의 위치, \(l_i\)는 첫 번째 \(w\) 타임스텝 동안 방문한 목표 위치의 수, \(s_i\)는 타임스텝 0에서의 위치입니다. \(P(w)\)는 타임스텝 0부터 모든 목표 위치를 방문하는 데 필요한 타임스텝보다 타임스텝 \(w\)부터 모든 목표 위치를 방문하는 데 필요한 타임스텝이 더 적은 에이전트의 수를 추정합니다. 우리는 \(P(w) \geq p\)가 될 때까지 \(w\)를 늘리고 윈도우드 MAPF 솔버를 계속 실행합니다. 여기서 \(p \in [0, m]\)는 사용자 지정 매개변수입니다. 이는 최소한 \(p\)명의 에이전트가 첫 번째 \(w\) 타임스텝 동안 (일부) 목표 위치를 방문하거나 다음 목표 위치에 더 가까워졌음을 보장합니다.
Example 3
그림 2c의 평생 MAPF 인스턴스를 다시 고려해 보십시오. \(p = 1\)이라고 가정합니다. 시간 지평선 \(w = 2\)인 경우, 예제 2에서 논의한 것처럼, 두 에이전트 모두 시작 위치에 머무르므로 \(P(2) = 0\)입니다. \(w\)를 3으로 늘리면, 윈도우드 MAPF 솔버는 에이전트 \(a_1\)에게 길이 3인 경로 [B, C, D, E]와 에이전트 \(a_2\)에게 길이 9인 경로 [C, D, E, ..., K, L]을 찾습니다. 이제 \(P(3) = 1\)인데, 이는 에이전트 \(a_1\)이 타임스텝 3에서 셀 E에 있고 목표 위치를 방문하는 데 추가적인 타임스텝이 0이기 때문입니다. \(P(3) = p\)이므로 윈도우드 MAPF 솔버는 이 경로 집합을 반환하고 교착 상태를 피합니다.
이러한 잠재적 함수를 설계하는 몇 가지 방법이 있습니다. 예를 들어, 타임스텝 \(w\) 이전에 도달한 목표 위치의 수 또는 타임스텝 \(w\)부터 모든 에이전트가 목표 위치를 방문하는 데 필요한 타임스텝의 합에서 타임스텝 0부터 모든 에이전트가 목표 위치를 방문하는 데 필요한 타임스텝의 합을 뺀 값 등입니다. 우리의 실험에서는 위에서 설명한 것만 사용합니다. 우리는 미래에 더 많은 잠재적 함수를 설계하고 그 효과를 비교할 계획입니다. (deadlock 을 피하는 다른 potential function들)
불행히도 교착 상태 회피 메커니즘을 가진 RHCR은 여전히 불완전합니다. 많은 에이전트가 수평으로 이동하지만 단 한 명의 에이전트만 수직으로 이동하고자 하는 교차로를 상상해 보십시오. 항상 수평 에이전트를 움직이게 하고 수직 에이전트를 기다리게 하면 처리량을 극대화하지만 완전성을 잃게 됩니다(수직 에이전트는 결코 목표 위치에 도달할 수 없습니다). 그러나 수직 에이전트를 움직이게 하고 수평 에이전트를 기다리게 하면 완전성을 보장할 수 있지만 처리량이 낮아집니다. 이 문제는 시간 지평선 \(w = \infty\)를 사용하더라도 발생할 수 있습니다. 처리량과 완전성이 서로 경쟁할 수 있기 때문에, 이 논문에서는 완전성 대신 처리량에 초점을 맞추기로 결정했습니다. (처리량과 완전성이 trade-off 이기 때문에 완전성이 보장이 안된다.)
Experiments 정리
RHCR을 C++로 구현하였으며, CBS, ECBS, CA*, PBS를 기반으로 한 네 가지 윈도우드 MAPF 솔버를 사용합니다. CA*와 PBS의 저수준 솔버로는 위치-시간 A*의 고급 변형인 SIPP(Phillips and Likhachev 2011)를 사용합니다. CBS와 ECBS에 대해서는 충돌 수가 적은 경로를 선호하는 경향이 있는 최근 변형인 Soft Conflict SIPP(SCIPP)(Cohen et al. 2019)를 사용합니다. 우리는 새로운 무작위 우선 순위 순서로 CA*를 반복적으로 재시작하는 CA*에 무작위 재시작을 사용하여, 해결책을 찾을 때까지 계속합니다. 또한 비교를 위해 기존의 방법(3)의 두 가지 실현, 즉 종단점 유지(Ma et al. 2017)와 더미 경로 예약(Liu et al. 2019)을 구현했습니다. 우리의 온라인 설정에서 작동하지 않기 때문에 방법(1)과 비교하지 않습니다. 다양한 방법의 스트레스 테스트를 위해 밀집된 환경을 선택했고, 밀집된 환경에서의 성능이 무한 시간 지평선을 가진 RHCR과 유사하기 때문에 방법(2)와 비교하지 않습니다. 각 실험에 대해 5,000 타임스텝을 시뮬레이션하며, 잠재적 함수 임계값 \(p = 1\)을 사용합니다. 모든 실험은 16GB 메모리를 가진 Amazon EC2 인스턴스 유형 "m4.xlarge"에서 수행됩니다.
5.1 Fulfillment Warehouse Application
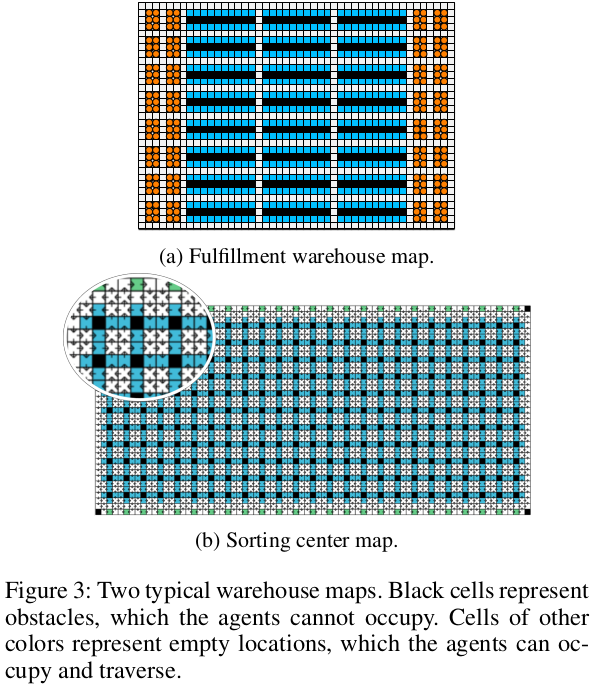
이 하위 섹션에서는 자동화된 창고에서 일반적인 충족 창고 문제를 소개합니다. 이 문제들은 지도 중앙에 인벤토리 포드의 블록과 주변에 작업 스테이션이 특징입니다. 방법(3)은 이러한 잘 형성된 인프라에서 적용 가능하며, 따라서 RHCR을 방법(3)의 두 가지 실현과 비교합니다. 우리는 (Liu et al. 2019)에서 가져온 그림 3a의 지도를 사용합니다. 이는 33 × 46 4-이웃 그리드로, 16%의 장애물이 있습니다. 에이전트의 초기 위치는 오렌지 셀에서 무작위로 균일하게 선택되며, 작업 할당자는 에이전트의 목표 위치를 파란 셀에서 무작위로 균일하게 선택합니다. RHCR에 대해, 우리는 시간 지평선 \(w = 20\)과 재계획 기간 \(h = 5\)를 사용합니다. 다른 두 방법에 대해서는 방법(3)이 요구하는 대로 매 타임스텝마다 재계획합니다. 모든 방법은 그들의 (윈도우드) MAPF 솔버로 PBS를 사용합니다.
표 1은 다양한 수의 에이전트 \(m\)을 가진 이 방법들의 처리량과 실행 시간을 보고합니다. 처리량 측면에서, RHCR은 더미 경로 예약 방법을 능가하며, 이 방법은 다시 종단점 유지 방법을 능가합니다. 이는 2.2절에서 논의된 바와 같이, 방법(3)이 일반적으로 그 해결책에서 불필요하게 더 긴 경로를 생성하기 때문입니다. 그러나 실행 시간 측면에서, 우리의 방법은 실행 당(즉, (윈도우드) MAPF 솔버 호출 당) 더 느립니다. 왜냐하면 경쟁 방법들은 일반적으로 5명 미만의 에이전트에 대해 재계획하기 때문입니다. 이 방법들의 단점은 매 타임스텝마다 재계획해야 하며, 더 낮은 처리량을 달성하고, 모든 지도에 적용할 수 없다는 것입니다.
5.2 Sorting Center Application
이 소절에서는 창고에서 흔히 발생하는 분류 센터 문제를 소개합니다. 이 문제들은 지도 중앙에 균일하게 배치된 슈트와 주변에 작업 스테이션들로 특징지어집니다. 이러한 인프라는 일반적으로 잘 형성된 구조가 아니기 때문에 방법(3)은 적용되지 않습니다. 우리는 그림 3b의 지도를 사용합니다. 이것은 37 × 77 4-이웃 그리드이며, 10%의 장애물이 있습니다. 상단 및 하단 경계의 50개의 녹색 셀은 사람들이 드라이브 유닛에 패키지를 올리는 작업 스테이션을 나타냅니다. 275개의 검은 셀(네 모서리 셀 제외)은 드라이브 유닛이 인접한 파란 셀 중 하나를 차지하고 슈트를 통해 패키지를 내려놓는 슈트를 나타냅니다. 드라이브 유닛은 녹색 셀과 파란 셀에 번갈아 할당됩니다. 시뮬레이션에서 작업 할당자는 파란 셀을 무작위로 균일하게 선택하고 드라이브 유닛의 현재 위치와 가장 가까운 녹색 셀을 선택합니다. 드라이브 유닛의 초기 위치는 빈 셀(즉, 검은색이 아닌 셀)에서 무작위로 균일하게 선택됩니다. 교환 충돌을 해결할 필요가 없게 하여 전체 프레임워크의 효율성에 초점을 맞출 수 있도록 이 지도의 방향 버전을 사용하여 MAPF 솔버를 더 효율적으로 만듭니다. 우리가 수작업으로 제작한 수평 방향은 왼쪽에서 오른쪽으로 이동하는 두 줄이 오른쪽에서 왼쪽으로 이동하는 두 줄과 번갈아가며, 수작업으로 제작한 수직 방향은 상단에서 하단으로 이동하는 두 열이 하단에서 상단으로 이동하는 두 열과 번갈아갑니다. 우리는 재계획 기간 \(h = 5\)를 사용합니다.
표 2와 3은 시간 지평선 \(w\)의 다양한 값에 대해 PBS, 1.1의 부최적 팩터를 가진 ECBS, CA*, CBS를 사용하는 RHCR의 처리량과 런타임을 보고합니다. 예상대로, \(w\)는 처리량에 크게 영향을 미치지 않습니다. 대부분의 경우, \(w\)의 작은 값은 \(w = \infty\)와 비교했을 때 처리량을 1% 미만으로 변경합니다. 그러나 \(w\)는 실행 시간에 큰 영향을 미칩니다. 모든 경우에서, \(w\)의 작은 값은 처리량을 저하시키지 않으면서 RHCR의 속도를 최대 6배까지 높입니다. \(w\)의 작은 값은 또한 에이전트 수에 대한 확장성을 제공하며, 이는 두 표에서 "미제공"으로 표시된 것으로 나타납니다. 예를 들어, \(w = \infty\)를 가진 PBS는 최대 700개의 에이전트 인스턴스만 해결할 수 있지만, \(w = 5\)를 가진 PBS는 최소 1,000개의 에이전트 인스턴스까지 해결할 수 있습니다.
5.3 Dynamic Bounded Horizons
이 논문에서는 평생 MAPF 문제를 해결하기 위해 롤링-호라이즌 충돌 해결(RHCR)을 제안했습니다. 이는 평생 MAPF를 일련의 윈도우드 MAPF 인스턴스로 분해합니다. 우리는 여러 일반적인 MAPF 솔버를 윈도우드 MAPF 솔버로 변환하는 방법을 보여주었습니다. RHCR은 완전성이나 최적성을 보장하지 않지만, 충족 창고 지도와 분류 센터 지도에서의 성공을 실증적으로 입증했습니다. 우리는 1,000개의 에이전트에 이르는 확장성을 보여주면서도 높은 처리량의 솔루션을 생성했습니다. 방법(3)과 비교할 때, RHCR은 일반 그래프에 적용되며 더 나은 처리량을 제공합니다. 전반적으로 RHCR은 일반 그래프에 적용되고, 사용자가 지정한 빈도로 재계획을 호출하며, 지속적으로 도착하는 새로운 목표 위치에 적응할 수 있는 유연한 계획을 생성할 수 있으며, 먼 미래를 예측하는 데 드는 계산 노력을 낭비하지 않습니다.
RHCR은 간단하고 유연하며 강력합니다. 평생 MAPF 문제를 해결하기 위한 새로운 방향을 제시합니다. 향후 작업의 여러 방향이 있습니다:
1. 혼잡도와 계획 시간 예산에 따라 시간 지평선 \(w\)를 자동으로 조정하는 것,
2. 에이전트를 그룹화하고 병렬로 계획하는 것, 그리고
3. 이전 검색에서 검색 노력을 재사용하기 위해 점진적 검색 기술을 배포하는 것입니다.
또한, 5.1절에서 언급된 60개의 에이전트가 있는 인스턴스에서 \(w = 5\)와 \(p = 60\)을 사용하는 RHCR로 교착 상태 회피 메커니즘을 사용하여 각 윈도우드 MAPF 에피소드에 대한 \(w\)의 값을 자동으로 결정할 수 있는지 평가합니다. 윈도우드 MAPF 솔버로 1.5의 부최적 팩터를 가진 ECBS를 사용합니다. 각 윈도우드 MAPF 에피소드에서 실제로 사용된 평균 시간 지평선은 9.97 타임스텝입니다. 처리량과 런타임은 각각 2.10과 0.35초입니다. 그러나 고정된 \(w\) (즉, \(p = 0\))를 사용하면 시간 지평선 \(w = 5\)에서 처리량 1.72와 런타임 0.07초, 시간 지평선 \(w = 10\)에서 처리량 2.02와 런타임 0.17초를 달성합니다. 따라서 이 동적 유한 시간 지평선 방법은 높은 처리량을 생성하는 좋은 지평선 길이를 찾을 수 있지만, 반복적으로 시간 지평선을 늘려야 하기 때문에 런타임 오버헤드가 발생합니다.
Conclusion
이 논문에서는 평생 MAPF를 일련의 윈도우드 MAPF 인스턴스로 분해하여 해결하는 롤링-호라이즌 충돌 해결(RHCR)을 제안했습니다. 우리는 여러 일반 MAPF 솔버를 윈도우드 MAPF 솔버로 변환하는 방법을 보여주었습니다. RHCR은 완전성이나 최적성을 보장하지는 않지만, 충족 창고 지도와 분류 센터 지도에서 그 성공을 경험적으로 입증했습니다. 우리는 1,000명의 에이전트까지 확장성을 입증하면서도 높은 처리량의 솔루션을 생산했습니다. 방법(3)과 비교할 때, RHCR은 일반 그래프에 적용될 뿐만 아니라 더 나은 처리량을 제공합니다. 전반적으로, RHCR은 일반 그래프에 적용되며, 사용자가 지정한 빈도로 재계획을 호출하며, 계속 도착하는 새로운 목표 위치에 적응할 수 있을 뿐만 아니라 먼 미래를 예측하는 데 드는 계산 노력을 낭비하지 않는 유연한 계획을 생성할 수 있습니다.
RHCR은 단순하고, 유연하며, 강력합니다. 평생 MAPF 문제를 해결하기 위한 새로운 방향을 제시합니다. 미래 연구의 많은 방향이 있습니다:
1. 혼잡도와 계획 시간 예산에 기반하여 시간 지평선 \(w\)를 자동으로 조정,
2. 에이전트를 그룹화하고 병렬로 계획, 그리고
3. 이전 검색의 검색 노력을 재사용하기 위한 점진적 검색 기술을 배포합니다.
'Paper Review > MAPF' 카테고리의 다른 글
| [Paper Review] 2019_[AAAI]Multi-agent pathfinding: Definitions, variants, and benchmarks (0) | 2024.01.31 |
|---|
