[Paper Review] 2023_[T-ITS]An Efficient Spatial-Temporal Trajectory Planner forAutonomous Vehicles in Unstructured Environments

 

 

 

 

- video: https://www.youtube.com/watch?v=X0V0bGuMsGg

- github: https://github.com/ZJU-FAST-Lab/Dftpav

GitHub - ZJU-FAST-Lab/Dftpav: A lightweight differential flatness-based trajectory planner for car-like robots

Abstract 정리

• 자율 주행 시스템의 중요한 구성 요소로서, 동작 계획은 학계와 산업에서 큰 관심을 받고 있습니다. 본 논문은 차량 형태의 간결한 볼록 근사를 활용하여 비구조적 환경에서 효율적이고 공간-시간적으로 최적의 궤적 최적화에 초점을 맞춥니다. 기존 방법론은 일반적으로 상태 구성 공간에서 운동 과정을 이산화하여 최적 제어 문제로 모델링합니다. 그러나 이는 종종 동적 과정의 고정밀 이산화가 필요하여 높은 품질의 운동 궤적을 생성하는 데 계산 부담이 상당하다는 점에서 최적성과 효율성 사이의 트레이드 오프로 이어집니다.(기존 방법의 한계점) 이 문제를 해결하기 위해 차량과 유사한 로봇의 미분 플랫성(differential flatness) 특성을 활용하여 궤적 표현을 단순화하고 비홀로노믹(differential) 역학의 가능성을 보장하면서 공간-시간적으로 연속적인 최적화 문제를 평탄한 출력을 이용해 콤팩트하게 분석적으로 구성합니다. 더불어, 모델링되지 않은 장애물에 대한 충돌 없는 주행 통로 및 동적인 이동 객체에 대한 부호 거리 근사를 통해 효율적인 장애물 회피를 달성합니다. (이 논문의 핵심 contribution) 우리는 효율성과 궤적 품질 측면에서 제안된 방법의 중요성을 보여주는 최첨단 방법들과의 포괄적인 벤치마크를 제시합니다. 실제 세계 실험은 우리 알고리즘의 실용성을 확인합니다. 우리는 연구 커뮤니티를 위해 우리의 코드를 공개할 예정입니다.

---

Introduction 정리

• 자율 주행은 최근 몇 년간 거대한 사회적 이점을 갖고 있기 때문에 가장 핫한 연구 주제 중 하나가 되었습니다. 복잡하고 고다이내믹 환경에서 견고하고 충돌 없는 동작 계획에 대한 엄청난 수요를 드러냅니다. 실제 응용 프로그램에서 경량화와 효율성은 제한된 기기 내 컴퓨팅 파워로 동적이고 구조화되지 않은 환경에 신속하게 대응하기 위해 강력하게 요구됩니다. 자율 주행의 동작 계획은 충돌 없이, 저에너지로, 물리적으로 실행 가능한 궤적을 생성하여 주체 차량이 제약된 환경에서 충돌 없는 보증과 설계된 속도로 최종 상태에 도달하도록 하는 것을 목표로 합니다. 고전적인 궤적 계획 방법은 주로 두 가지 주요 그룹으로 분류됩니다: 샘플링 기반 방법과 최적화 기반 방법입니다. 샘플링 기반 방법은 일련화된 상태 공간에서 샘플을 생성하고 이러한 샘플의 비용 함수를 평가하여 경로를 얻습니다. 반면에, 최적화 기반 방법은 궤적 계획을 최적화 문제로 정의하고 최적의 해결책을 찾기 위해 기울기 기반의 숫자 해결자를 활용합니다. 샘플링 기반 방법은 이론적으로 해상도를 완성하고 최적의 해결책을 얻기 위해 전체 상태 공간을 탐색할 수 있지만, 이는 종종 계산 비용이 많이 듭니다. (기존 방법의 문제점) 따라서 이 논문에서는 연속 공간에서 궤적이 강한 변형 능력을 갖도록 함으로써 지역 최적 솔루션에 정확하고 효과적으로 수렴할 수 있는 최적화 기반 방법에 중점을 두었습니다. (이 논문의 장점) 그러나 임의적으로 복잡한 시나리오에서 온라인으로 실행 가능하고 고품질의 궤적을 생성하는 것은 여전히 도전적입니다. (기존 방법론의 한계점) 사실, 자율 주행을 위한 이상적인 동작 계획은 일반적으로 세 가지 도전적인 문제에 직면하게 됩니다:
  
  • 비홀로노믹 다이내믹스: 초등 이동 로봇과 쿼드로터와 같은 홀로노믹 로봇과 달리, 자율 주행 차량은 궤적 계획 중 비홀로노믹 제약 조건을 고려해야 합니다. 또한, 비홀로노믹 다이내믹스의 강한 비볼록성과 비선형성으로 인해 고도로 제한된 환경에서 상태와 제어 입력의 물리적 실행 가능성을 보장하는 것이 어렵습니다.
    
    
  • 정확한 장애물 회피: 충돌 없는 제약 조건은 온라인 차량 재계획을 위해 물체 모양 모델링의 정확성을 유지하면서 합리적인 계산 시간을 유지해야 합니다. 현실 세계 응용에서는 자기 차량 모양의 대략적 근사치(예: 하나 또는 여러 개의 원 모양)는 항상 해결 공간을 축소시키므로, 이는 보수적이거나 극도로 혼잡한 지역에서 충돌 없는 해결책을 찾지 못할 수 있습니다. 반면, "전체 차원의 장애물 회피"로 알려진, 유클리드 공간에서 장애물의 실제 물리적 모양을 고려하는 것은 계획 문제의 복잡성을 증가시켜 중요한 계산 부담을 초래합니다.
    
    
  • 궤적 품질: 계산 효율성과 궤적 품질 사이에는 항상 균형이 필요합니다. 시간과 공간을 별도로 최적화하는 일반적인 방법은 특히 고도로 동적인 환경과 같은 밀접하게 결합된 공간-시간 시나리오에서 해결 공간의 큰 부분을 축소시킵니다. 이와 달리, 공간-시간 합동 최적화는 해결 공간을 완전히 활용하여 궤적 최적성을 향상시킬 수 있지만, 최적화 문제를 복잡하게 만들어 실시간 성능을 저하시킬 수 있습니다.

• 기존 방법들은 효율성, 고품질, 일반적인 적용 가능성 사이에서 좋은 균형을 달성하지 못하는 경우가 많습니다. 이러한 복잡한 도전에 따라 일부 방법들은 운동 모델을 지나치게 단순화하여 대형 회전이 필요한 경우 실행 불가능한 궤적을 생성하는 등의 문제가 발생합니다. 장애물 회피를 과도하게 단순화하는 방법도 있으며, 사전 정의된 규칙에 지나치게 의존하여 더 복잡하고 다양한 시나리오로의 확장이 제한됩니다. 또한, 대부분의 방법은 운동 과정을 이산화하는데, 이는 극도로 제한된 시간 내에 우수한 궤적을 생성하는 것을 어렵게 만듭니다. 밀집된 환경에서 궤적을 효과적으로 실행 가능하게 하고 높은 계획 성공률을 달성하기 위해 이러한 방법들은 종종 고정밀 이산화를 필요로 하며, 이는 상당한 컴퓨팅 요구를 가지고 실시간 성능을 저해합니다. (기존 방법론들의 단점) 전반적으로 궤적 계획에 대한 보편적인 해결책이 없어, 이는 자율 주행의 발전을 저해하는 취약점이 됩니다.
  
  이러한 간극을 메우기 위해, 우리 논문은 차량 형상의 간단한 볼록 근사를 기반으로 하는 효율적이고 다용도 공간-시간 궤적 계획 체계를 제안합니다. 이는 제약된 환경에서 비홀로노믹 다이내믹스를 준수하는 고품질 궤적을 생성합니다(그림 1 참조). (이 논문의 장점) 평면 공간에 기반하여, 우리는 궤적을 형식적으로 매개변수화하기 위해 piece-wise polynomial을 사용하고, 궤적 표현을 재구성하여 등식 제약을 제거하고 최적화 문제를 단순화합니다. 더불어 최적화 문제에서 모든 실행 가능성 제약 조건을 최종 재정립된 최적화 변수의 해석적 형태로 인코딩합니다. gradient-based numerical solutions을 용이하게 하기 위해 제약 조건, 고차 상태, 평탄 출력, 다항식 표현 공간 및 궁극적으로 재구성된 최적화 변수를 포함한 완전한 기울기 역전파 체인을 해석적으로 유도합니다. (고품질 궤적을 생성하기 위한 방법론)
  
  중요한 점은 다방향 로봇과는 달리 차량 궤적은 전진 및 후진 동작이 동시에 존재하는 부분적으로 매끄러운 특성을 보입니다. 여기서 전진 및 후진 동작 사이의 전환점을 Gear Shifting Point (GSP)로 지칭합니다. 이 문제를 해결하기 위해, 우리는 전방 및 후방 움직임을 각각 매개변수화하기 위해 piece-wise polynomial을 사용합니다. 구체적으로, 다음 piece-wise polynomial의 시작점은 GSP인 이전 조각의 끝점입니다. 이전 작업과 달리 piece-wise polynomial의 초기 및 최종 지점이 고정되어 있는 것 대신, GSP와 다항식 매개변수 사이의 관계를 분석합니다. 그런 다음 추가적인 제약 조건을 도입하지 않고도 궤적 품질을 크게 향상시키는 Gear Shifting Point Optimization (GSPO)을 소개합니다. 또한, 정적 장애물 회피 제약을 위해 충돌 없는 기하학적 공간을 사용하고, 주체 차량과 다른 동적 객체 간의 부호 거리에 기반하여 동적 충돌 없음 속성을 보장합니다. 벤치마크와 실제 세계 실험은 우리 방법의 고급 및 실용적 성격을 확인합니다. 이 논문의 주요 기여 사항은 다음과 같이 요약될 수 있습니다:
  
  
  • 우리는 차와 유사한 로봇을 위한 통합 및 효율적인 궤적 계획 수식화를 제안하며, 이는 공간-시간적인 결합 최적화, 볼록 근사 기반의 정적 및 동적 장애물 회피, 평탄한 공간에서의 해석적인 제약식 표현, 그리고 효율적인 궤적 표현이라는 네 가지 필수적인 특성을 포함합니다. 구체적으로, 우리는 정제된 궤적 표현을 차량에 확장하여 움직임의 연속성을 보장하고 최적화 문제의 차원을 줄입니다. 또한, 모든 제약 사항은 궤적 표현 매개 변수로 재정립된 최적화 변수로 표현될 수 있습니다. 더 나아가, 우리는 완전한 기울기 역전파 체인을 유도하여 이후의 숫자적 해결을 용이하게 합니다.
    
    
  • 저희는 궤적 계획 문제의 제약 사항의 특성을 분석하고 원래의 최적화 문제를 효과적으로 해결할 수 있는 unconstrained 문제로 재정립합니다. 게다가, 우리는 GSPO(기어 전환 지점 최적화)를 소개하여 전진 및 후진 모션 간의 전환으로 인한 불연속성을 처리합니다. 우리의 방법은 궤적 매개 변수 공간에서 GSP(기어 전환 지점)을 자유 최적화 변수로 포함하여 궤적의 자유도를 증가시키고 초기 값에 대한 의존성을 감소시켜 궤적의 품질을 향상시킵니다.
    
    
  • 엔지니어링적인 측면에서, 저희는 우리의 접근 방식의 우수성을 증명하기 위해 시뮬레이션에서 넓은 범위의 비교 실험을 수행했습니다. 더불어 상업용으로 운용되는 유인 플랫폼에 알고리즘을 배포하고 복잡한 환경에서의 실제 실험을 통해 우리 알고리즘의 실용성을 입증했습니다. 게다가, 차량 모션 계획의 발전을 위해 우리의 계획 알고리즘을 완전히 오픈소스로 공개했습니다. 1

---

Related Works 정리

Trajectory Generations for Vehicles

• 샘플링 기반 및 탐색 기반 방법[11], [12], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24]은 사용자 정의 목표를 쉽게 통합할 수 있는 특성으로 로봇 모션 계획에 널리 사용되고 있습니다. 격자 기반 플래너[11], [12], [13], [14]는 연속 상태 공간을 격자 그래프로 이산화하여 계획합니다. Safe Interval Path Planning (SIPP) 및 해당 변형들[22], [23], [24]은 동적 장애물 회피를 위해 시간 공간을 실행 가능한 시간 간격으로 분해합니다. 그런 다음 Dijkstra 및 A*와 같은 그래프 탐색 알고리즘을 사용하여 그래프에서 최적의 경로를 찾습니다. Ren 등[23]은 SIPP를 확장하여 SIPP의 안전 간격 개념 및 다중 목적 탐색 기술을 활용하여 다중 목적 경로 계획을 처리합니다. Alabedeen Ali 및 Yakovlev [24]은 SIPP에 동역학 제약을 효과적으로 통합하여 실용성과 완성도를 개선합니다. 확률적 플래너[15], [16], [17], [18], [19], [20], [21]인 RRT(랜덤 트리 탐색)[15] 등은 시작 노드에서 루트되는 상태 트리를 확장하여 실행 가능한 경로를 얻습니다. 비 Convex 공간에서 국소 최소값을 피할 수 있는 능력에도 불구하고 이러한 전형적인 방법들은 실행 가능한 경로를 찾기 위해 이산적인 로봇 상태 공간에서 샘플링을 필요로 하며, 이는 계산 리소스와 경로 품질 사이의 딜레마를 야기합니다. 경로와 모션 모델 간의 정렬을 개선하기 위해 이러한 방법들은 종종 고차원 상태 공간에서 샘플링을 요구하며, 이는 조합 폭발로 이어질 수 있습니다. 이러한 방법들은 이론적으로 최적성을 보장하지만, 이러한 보장을 달성하려면 고해상도 샘플링 및 상당한 샘플 수가 필요하며, 이는 상당한 계산 부담을 야기합니다. (샘플링 방법의 장점이자 한계점) 시간과 경로 품질 간의 트레이드 오프로 인해 이러한 방법들이 복잡한 환경에서 효율적으로 고품질의 경로를 생성하는 데에 어려움이 있습니다.
• 경로 생성 문제를 간소화하기 위해 어떤 직관적인 방법들[26], [27], [28]은 경로의 공간 모양과 동적 프로파일을 분리합니다. Zhu 등[26]은 고정된 경로 길이로 곡률 제약의 비 볼록성을 제거하고 원래 문제를 이차 제약 이차 프로그램(QCQP)으로 변환하는 볼록 탄성 밴드 스무딩(CES) 알고리즘을 제안합니다. 그러나 작업 [28]에서 제시된 것처럼, 길이 일관성 가정이 항상 유지되지 않아 곡률 제약을 무효화시키고 이로 인해 제어의 실행 가능성이 줄어듭니다. CES 프레임워크를 기반으로 Zhou 등[28]은 순차적 볼록 최적화(SCP)를 사용하여 곡률 제약을 완화하여 매끄럽고 안전한 경로를 생성하는 이중 루프 반복 기반 경로 스무딩(DL-IAPS) 알고리즘을 제안합니다. 하지만, 이 방법의 효율성은 주로 hybridA*[29]로 얻은 초기 경로에 의존하므로 복잡한 환경에서의 적용을 제한합니다.
• 고도로 적응 가능한 모델 예측 제어(MPC) 방법은 경로 계획 문제를 최적 제어 문제(OCP)로 정식화하고 이를 비선형 프로그래밍(NLP) 문제로 더 이산화합니다. 이러한 접근 방법들[6], [7], [8], [9], [10], [30], [31], [32], [33], [34]은 이산적 상태 및 제어 입력을 최적화하여 동적 및 충돌 회피 제약을 편리하게 통합할 수 있습니다. 작업 [33]에서는 반복 최적화 프레임워크를 제안하여 초기 corridor에 대한 강건성을 향상시키고 경로 품질을 향상시킵니다. 작업 [34]에서는 다중 상황 제약 OCP를 구축하여 adaptive gradient-assisted particle swarm optimization algorithm을 사용하여 거의 최적의 참조 솔루션을 생성하고, 내부 경사 기반 최적화 계층에서 더 최적화합니다. 위의 MPC 기반 방법은 로봇의 모션 모델을 쉽게 수용할 수 있지만, 경로가 이산적 상태로 표현되기 때문에 제한된 환경에서의 경로 제약을 보장하기 위해서는 성능 저하를 감수하고 상태 밀도를 증가시켜야 합니다. (MPC 방법의 문제점)
• 몇몇 연구들[35], [36], [37], [38], [39]은 모션 플래닝에서 딥 뉴럴 네트워크(DNNs)의 잠재력을 보여줍니다. Qureshi 등[35]는 환경 네트워크(Enet)와 계획 네트워크(Pnet)로 구성된 모션 플래닝 네트워크를 제안합니다. Enet은 환경 특징을 추출하고, Pnet은 다음 후보 상태를 출력하는 데 사용됩니다. Chai 등[37]는 주차 조작에서 시스템 상태-제어 동작 사이의 기능적 관계를 학습하기 위해 미리 계획된 최적 주차 경로 데이터 세트를 사용하여 여러 DNN을 훈련시키고, DNN 성능을 향상시키기 위해 데이터 집합 방법을 설계합니다. 이 작업[37]은 기계 최적화된 시스템 상태와 제어 쌍 사이의 내재된 관계를 완전히 활용할 수 있는 순환 DNN을 설계함으로써 확장되었습니다[39]. 또한, 두 가지 전이 모델 전략이 제안되어 플래너를 다양한 차량 유형에 적응 가능하게 만듭니다. 학습 기반 방법은 특정 작업에서 효과적임을 보여주지만, 알려지지 않은 시나리오에 대한 견고성이 제한될 수 있습니다. 또한, 이러한 방법들은 효율성을 달성하기 위해 고성능 GPU 병렬 컴퓨팅이 필요합니다. 또한, 그들은 일반화를 위해 대량의 데이터가 필요하며, 이는 실용성을 제한할 수 있습니다. (Learning-base algorithm의 단점)

Obstacle Avoidance Formulation

• ego 차량 및 다른 장애물의 모델링은 경로 생성 문제의 충돌 방지 제약의 복잡성을 결정합니다. Li 등[33]은 ego 차량을 중앙선을 따라 두 개의 원으로 덮고, 그런 다음 장애물을 부풀려 자아 차량 모델을 두 점으로 단순화합니다. 작업[33]에서는 이 두 점을 안전 복도 내에 제약하여 장애물 회피를 보장합니다. 이 접근 방식은 본질적으로 충돌 방지 제약의 차원이 장애물 수와 독립적인 특성을 가지고 있습니다. 그러나 이러한 점 기반 모델링 방법은 솔루션 공간을 완전히 활용하지 않으며, 특히 복잡한 환경에서 과도하게 보수적인 경로를 생성하는 경우가 많습니다. (차량을 원으로 모델링하는 방법론의 단점)
  
  
• [9]에서는 임의로 배치된 장애물을 고려하여, 비구조화된 환경에서 경로 생성을 위한 통합 OCP로 문제를 정식화했습니다. 그러나 충돌 방지 제약은 명목적으로 미분 가능하지 않습니다. Zhang 등[40]는 장애물을 볼록으로 가정하고 최적화 기반의 충돌 회피 (OBCA) 알고리즘을 제안했는데, 이는 완전한 차원의 객체 충돌 회피를 모델링하는 데 사용되는 정수 변수를 제거합니다[41]. 그들은 로봇과 장애물 사이의 거리를 다시 정의하기 위해 이중 변수를 도입하고, 충돌 방지 제약을 연속적이고 미분 가능한 형태로 변환합니다. Zhang 등[31]은 운동 계획의 MPC 문제에 OBCA를 통합하여, 비구조화된 환경에서의 경로 계획을 위한 계층적 프레임워크 인 H-OBCA를 제안했습니다. 게다가, 최적화를 가속화하기 위해 이중 변수의 초기값을 설정하는 합리적인 방법이 작업 [31]에서 제시되었습니다. 그러나 OBCA 기반 방법에서 이중 변수를 도입하면 문제의 차원이 증가하여 해결이 더 어려워집니다. 또한 이중 변수의 수는 장애물 수와 긍정적으로 관련되어 있습니다. 장애물이 증가함에 따라 문제의 차원이 급격하게 증가하면서 수용할 수 없는 계산 및 메모리 비용이 발생합니다. (OCP를 사용한 OBCA의 문제점)
  
  
• 본 논문에서는 이론적 보장과 연속 공간에서 지역 최적 솔루션으로 정확하게 수렴하는 능력을 감안하여 최적화 기반의 경로 계획에 중점을 두었습니다. 특정 작업 기능을 활용하거나 인위적으로 정의된 규칙에 의존하는 대신, 저희 플래너는 충분히 일반적이며 복잡한 시나리오에 적응 가능한 강력한 특성을 갖고 있습니다. 전체적으로 계획 상태를 샘플링하거나 공간과 시간을 분리하거나 모션 모델을 이산화하거나 환경 특성에 많이 의존하는 대신, 저희 방법은 공간-시간 통합 최적화를 통해 전체 차원의 장애물 회피를 보장하면서 효율적으로 고품질 경로를 생성 (이 논문의 장점)합니다. 저희 방법은 낮은 계산 비용과 비구조화된 환경에서의 높은 견고성을 가지며, 더 자세한 정량적 비교는 제7절에서 제시됩니다.

---

Methodology 정리

• 이 섹션에서는 궤적 계획을 위한 공간-시간 합동 최적화 공식을 제시합니다. 최적화 공식을 구축하기 위해 전체 모션 플래닝 파이프라인을 논의하고 자동차 유형의 로봇에 대한 미분 플랫 모델을 소개합니다. 그런 다음, human comfort, 실행 시간 및 실행 가능성 제약 조건을 고려한 궤적 최적화 문제의 공식화를 보여줍니다. 마지막으로, 이후의 숫자적 최적화를 위한 문제의 그래디언트 전파 체인을 분석합니다.

A. Planning Pipeline

• 저희 방법론은 전체적으로 전단단 계층 구조를 따릅니다. 프론트엔드는 초기 추정치를 제공하는 주된 역할을 하고, 백엔드 최적화가 이어집니다. 저희는 경량 hybridA* 알고리즘을 채택하여 충돌 없는 경로를 찾고, 이를 제안된 플래너에 의해 추가적으로 최적화합니다. 알고리즘의 구현에서, 로봇의 상태는 위치와 방향 각도로 정의됩니다. 또한, 각 확장 상태마다 검색 프로세스를 조기에 종료하기 위해 Reed Shepp Curve [42]를 사용하여 끝 상태를 시도합니다. 자율 주행 주차와 같은 복잡한 운전 작업의 경우, 프론트엔드 출력에는 종종 전진 및 후진 차량 운동이 모두 포함됩니다. 기어 변속 위치에서 차량이 항상 완전히 정지한다고 합리적으로 가정하면, 전방 및 후방 세그먼트를 각각 구간 다항식으로 매개변수화하고 이에 대한 구체적인 공식은 III-C 섹션에서 제시됩니다. 또한, 각 세그먼트의 운동 방향은 프론트엔드 출력에 의해 결정되며, 백엔드 최적화 프로세스 이전에 미리 설정됩니다.

B. Differentially Flat Vehicle Model

• 저희는 단순화된 기구적 자전거 모델을 카테시안 좌표계에서 사용하여 네 개 바퀴 차량을 설명합니다. 차가 전륜 구동이며 완벽한 롤링과 미끄러짐 없이 조향되었다고 가정하면, 모델은 Fig. 2와 같이 설명될 수 있습니다. 상태 벡터는 $x = (p_x , p_y , \theta, v, a_t , a_n , \phi, \kappa)^{T}$ 로, 여기서 $p = (p_x , p_y)^{T}$는 후륜 중심의 위치를 나타내며, $v$는 차체 프레임에 대한 종방향 속도, $a_t$는 경도 가속도를 나타내고, $a_n$은 위도 가속도를, $\phi$는 전륜의 조향 각도를, $\kappa$는 궤적의 즉각적 곡률을 나타냅니다. 차량 모델에 대한 철저한 연구 덕분에 [43], 우리는 평평한 출력을 $\sigma := \sigma_x ,\sigma_y$ 로 선택했는데, 이는 $\sigma = p$ 가 차량의 후륜을 중심으로 한 위치를 의미합니다. $p_x , p_y$ 를 제외한 다른 변수 변환은 다음과 같이 표현될 수 있습니다:

• 결과적으로, 자연스러운 미분적 평평성 특성을 가지고 있기 때문에, 우리는 평평한 출력과 그들의 유한 미분을 사용하여 차량의 임의의 상태량을 특성화할 수 있습니다. 이것은 궤적 계획을 단순화하고 최적화를 용이하게 합니다. 우리는 차량의 운동 방향을 특성화하기 위해 $\eta \in \{−1, 1\}$의 추가적인 변수를 정의합니다. 여기서 $\eta = −1$은 후진 운동을, $\eta = 1$은 전진 운동을 나타냅니다. 기어 이동 시 속도 크기를 작은 0이 아닌 상수로 고정함으로써 특이점을 피합니다. 기어 이동 위치와 방향 각도는 최적화될 수 있으며, 이에 대한 구체적인 공식은 VI 섹션에서 제시됩니다.

C. Optimization Formulation

i번째 궤적 세그먼트는 2차원 공간에서 시간에 대해 균일한 \( M_i \)-조각 다항식으로 표현되며, 각 조각은 \( N = 2s-1 \) 차수로, 중간 경유점 \( q_i = (q_{i,1}, \ldots, q_{i,M_i-1}) \)에 의해 매개변수화됩니다. 이는 \( \mathbb{R}^{2 \times (M_i-1)} \)에 속하며, 각 조각의 시간 간격 \( \delta T_i \)는 \( \mathbb{R}_+ \)에 속하고, 계수 행렬 \( c_i = (c_{i,1}^T, \ldots, c_{i,M_i}^T)^T \)는 \( \mathbb{R}^{2M_i \times 2} \)에 속합니다. 그러면 i번째 세그먼트의 j번째 조각 \( \sigma_{i,j}(t) \)는 다음과 같이 쓸 수 있습니다:

여기서 \( \beta(t) \)는 자연 기저이며, \( n \)은 궤적 세그먼트의 수입니다. 그리고 \( \sigma_i(t) \)는 다음과 같이 얻어집니다:

여기서 모든 \( j \)에 대해 \( 1 \leq j \leq M_i \), 그리고 \( t \)에 대해 \( [ (j-1) \times \delta T_i, j \times \delta T_i ] \)에 속합니다.

전체 궤적 \( \sigma(t) \)는 다음과 같이 형성됩니다:

여기서 \( \hat{T}_i \)는 시작점의 타임스탬프입니다. 또한 계수 세트 \( c = (c_1^T, c_2^T, \ldots, c_n^T)^T \)를 정의하고, 총 시간 세트 \( T = (T_1, T_2, \ldots, T_n)^T \)를 도입합니다. 이후 유도되는 데 사용됩니다. 장애물 회피와 동적 실행 가능성 제약 조건과 함께, 시간 정규화를 포함하는 최소 제어 노력 문제는 다음과 같은 비선형 제약 조건 최적화 문제로 표현될 수 있습니다:

W는 대각 행렬로 제어 노력을 penalize하기 위해 사용됩니다. 식 (5c)는 경계 조건이며, 여기서 \( \sigma_0, \sigma_f \)는 사용자가 지정한 초기 및 최종 상태입니다. \( \sigma_i \)는 GSP에서의 전환 상태입니다. 견고성을 높이기 위해 궤적의 위치와 접선 방향이 최적화되고, 가속도는 제로로 고정되어 있어 요동을 방지합니다. 또한 제약 조건 식 (5d)의 구체적인 형식과 해당 최적화는 섹션 VI-C에서 자세히 설명됩니다. 식 (5e)는 \( \tilde{d} \) 차수까지 연속성 제약 조건입니다. 목적 함수의 두 번째 항 \( w_T T_s \)는 시간 정규화 항으로 전체 시간 \( T_s \)를 제한하기 위한 것입니다. 제약 함수는 \( G_d \)로 정의되며, 우리의 형식화에서 집합 \( D = \{ d : d = v, a, a_n, k, \xi, \Omega \} \)는 동적 실행 가능성(속도 \( v \), 가속도 \( a \), 저크 \( a_n \), 경계 \( k \), 정적 및 동적 장애물 회피 \( \xi, \Omega \))을 포함합니다. 게다가 \( s \)는 3으로 선택되었는데, 이는 저크의 적분이 최소화되어 인간의 안락함을 보장하기 위함입니다.

D. Gradient Derivation

여기에서는 최적화 문제에서 목적 함수와 제약 조건의 그라디언트(미분)를 계산하는 방법에 대해 설명하고 있습니다. 특히, 주어진 궤적 세그먼트에 대한 다항식 표현과 이를 사용하여 연속적인 제약 조건을 이산적으로 근사하는 방법을 다루고 있습니다.

먼저, 목적 함수 \( J \)에 대한 각 다항식 조각의 계수 \( c_{i,j} \)와 각 조각의 시간 간격 \( T_i \)에 대한 그라디언트를 계산합니다. 이를 위해 베타 함수 \( \beta(t) \)와 각 다항식 조각을 사용합니다. 그라디언트 계산은 연쇄 법칙(chain rule)을 사용하여 이루어집니다.

제약 조건 \( G_d \)는 궤적이 장애물을 피하고 동적 실행 가능성을 만족하도록 합니다. 연속적인 제약 조건 \( G_d(\sigma(t), ..., \sigma^{(s)}(t)) \leq 0 \)를 근사하기 위해, 궤적을 여러 개의 이산적인 점으로 나누고 각 점에서 제약 조건을 적용합니다.

여기서 \( \bar{t} \)는 상대적 타임스탬프이고 \( \hat{t} = \hat{T}_i + \delta T_i \times (j - 1) + \bar{t} \)은 절대적 타임스탬프입니다. 따라서, 연속 시간 수식인 식 (8)을 근사하기 위해서, 우리는 조각별 다항식의 각 부분을 \( \lambda \in \mathbb{N}_{>0} \) 제약점들로 균일하게 이산화합니다. 더욱이, 우리는 이 제약점들에 제약을 부과함으로써 궤적의 실행 가능성을 보장합니다. 그런 다음 연속 시간 수식인 식 (8)은 이산 형태로 변환됩니다:

그라디언트 계산은 다음과 같이 이루어집니다:

모든 위의 그라디언트 계산은 벡터들에 대해 분모 레이아웃을 따릅니다. 결과적으로, 식 (12)-(14)를 식 (11)에 대입함으로써, \( G_{d,i,j,k} \)의 그라디언트를 \( c_{i,j} \)와 \( T \)에 대해 얻을 수 있습니다. 일단 \( \partial G_{d,i,j,k} / \partial \sigma_{i,j,k}^{(\bar{d})} \)와 \( \partial G_{d,i,j,k} / \partial \hat{t} \)가 명시되면 말이죠. 게다가, 제약 함수 \( G_{d,i,j,k} \)는 \( \hat{t} \)와 \( \sigma_{i,j,k}^{(\bar{d})} \)에 있는 몇몇 양에 의해 정확히 표현될 수 있습니다. 여기서 \( \bar{d} \)는 \( \{0, 1, 2, \ldots, s\} \)에 속합니다. 그러므로, 관련 없는 변수들에 대한 그라디언트는 유도 없이 0입니다.
이후 섹션에서, 우리는 제약 함수 \( G_{d \in D} \)의 구체적 형식을 제시하고 그라디언트를 유도할 것입니다. 단순화를 위해, \( i, j, k \)와 상대적 타임스탬프 \( \hat{t} \)는 섹션 IV와 섹션 V에서 생략됩니다.

IV. INSTANTANEOUS STATE CONSTRAINTS

A. Dynamic Feasibility

(자세한 내용은 생략; 논문 참고)

 

1) Longitude Velocity Limit

2) Acceleration Limit

3) Front Steer Angle Limit

B. Static Obstacle Avoidance

• 이 하위 섹션에서 우리는 환경의 자유 공간의 기하학적 표현을 기반으로 효율적으로 계산 가능한 정적 충돌 방지 제약 조건을 분석적으로 제시합니다. (1)우리는 먼저 의미 있는 환경을 분해하고 충돌이 없는 공간을 추출하여 일련의 볼록 다각형으로 구성된 주행 corridor를 구성합니다. (2)그런 다음, 주행 corridor 내에서 전체 차량 모양을 강제하는 데 필요한 충분조건과 필요조건을 도출하여 정적 충돌 방지 제약 조건을 구성합니다. 구체적인 유도에 앞서 제약 모델링 파이프라인을 소개합니다. (1)먼저, 프론트 엔드에서 생성된 충돌이 없는 경로를 후단 최적화의 제약점 수와 동일한 수의 샘플링 지점으로 이산화합니다. (2)그런 다음, 환경 정보와 결합하여 각 정의된 방향으로 직접 확장하거나 [45]의 방법을 사용하여 샘플링 지점을 기반으로 자유 볼록 다각형을 생성합니다. 결과적으로, 전체 차량 모양을 각 제약점에서 해당 볼록 다각형에 제약함으로써 전체 궤적이 충돌 없음을 보장합니다. 이것은 Fig. 3에 나타난 것처럼 됩니다. 우리는 ego 차량의 전체 모양을 둘러싸기 위해 볼록 다각형을 사용하고, 이는 E로 정의되며, 볼록 다각형의 꼭짓점 집합 E를 정의합니다:

(자세한 내용은 생략; 논문 참고)

 

V. DYNAMIC OBSTACLE AVOIDANCE

• 동적 충돌 방지 속성은 궤적의 각 순간에 거리가 충돌 방지 임계값보다 큰 것을 보장함으로써 ego 차량과 장애물 볼록 다각형 간의 최소 거리를 확보함으로써 보장됩니다. 가독성을 높이기 위해 볼록 다각형 사이의 부호 있는 거리를 평가하는데 도움이 되는 사전 정보를 도입합니다. 그런 다음, 연속적으로 미분 가능한 형태로 더 완화된 동적 회피 제약 조건 함수에 대해 자세히 설명합니다.

A. Preliminaries on Distance Representations

1) Signed Distances for Rigid Objects

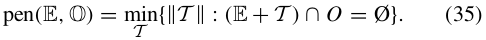
• (34), (35)는 자차의 vertices에서 obstacle의 vertices까지의 최소 거리를 나타냄.
• signed distance를 계산하기 위해서는 최소 최적화 문제를 해결해야 하는데, 이는 저희의 궤적 최적화 문제에 포함하기에 적합하지 않습니다. 다음 섹션에서는 부호 있는 거리를 대략적으로 효율적으로 계산하기 위한 Minkowski difference-based algorithm에 대해 논의하겠습니다.

2) Approximation Distances

Minkowski difference

• Minkowski difference에 의해 signed distance between ego and obstacle vertices의 거리를 원점에서 부터의 거리로 변경 가능.

• 자차의 hyperplane으로부터 타차의 vertices까지의 거리와 ego의 vertices에서 부터 타차의 hyperplane까지의 minkowski difference의 최대값이 실제 거리보다 작거나 같다.

• (40)식에서 위에 식은 자차의 hyperplane 안에있는 어떠한 $\mathbf{y}$ vector와 타차의 vertices와의 차이를 나타내는 $\mathbf{p}$ matrix를 나타냄. (40)식에서 밑에 식은 자차의 hyperplane식에서 양쪽에 $(\textbf{H}^e)^T \mathbf{p}$를 더한 식과 같다. (저렇게 식을 만들어서 $\mathbf{u}$에 대한 식으로 바꾸는게 목적)

(42)번 식은 결국 obstacle의 vertices중에 Minkowski difference의 원점과 가장 가까운 vertex까지의 거리이고 (43)번 식은 자차의 vertices중에 Minkowski difference의 원점과 가장 가까운 vertex까지의 거리다.

B. Constraint for Dynamic Avoidance

dynamic collision-free constraint

• $d_m$은 minimum collision-free distance이다.

collision avoidance를 하기 위해서는 자차의 모든 vertices와 타차의 모든 vertices의 signed distance의 거리가 lower bound signed distance 거리보다 커야한다.

Lower bound는 (39)번 식으로부터 도출되어 (46)번 식으로 구해진다. 이는 원점으로부터의 타차의 vertices와 자차의 hyperplanes의 차이까지의 거리 (즉, Minkowski difference)와 원점으로부터 타차의 hyperplanes과 자차의 vertices와의 차이까지의 거리중에 최대 값이 된다. (즉, 자차와 타차의 거리중에 최대 거리보다는 자차와 타차의 거리가 멀어야 한다는 말)

Hyperplane descriptor

$B$가 곱해진 이유는 $\mathbf{H}^e$ 가 hyperplane의 normal vector이기 때문이다.

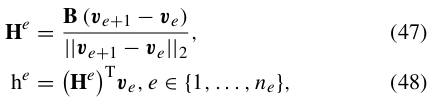
(42)번 식은 vertices로 표현된 (49)번식으로 변경가능하다.

(47)식과 비슷하게 자차와 타차의 hyperplane을 같이 표현하는 식 (50)

위 (46)번 식은 각각 (51)과 (52)로 풀어 쓸 수 있으며 이 식들을 대입하여 (53)번 식을 만들 수 있다. 여기서 갑자기 min 앞에 max가 튀어나온 이유는 원점으로 부터의 거리가 아니라 각 vertices까지의 거리이기 때문에 최소값을 구하기 위해서는 마이너스 vertices에는 max를 해줘야하기 때문이다.

 

"log-sum-exp" 함수의 변형된 형태를 설명하고 있습니다. 이 함수는 벡터 내의 최대값 또는 최소값을 부드럽게 근사화하는데 사용됩니다. 기본적인 "log-sum-exp" 함수는 최대값을 근사하는데 사용되지만, 여기서 제시된 형태는 스칼라 매개변수 \( \alpha \)를 사용하여 최대값과 최소값 모두를 근사할 수 있습니다. 함수의 정의는 다음과 같습니다:

\[ lse_{\alpha}(\mathbf{y}) = \alpha^{-1} \log\left( \sum_{\omega=1}^{\Omega} \exp(\alpha r_{\omega}) \right) \]
여기서 \( \mathbf{y} = \{r_1, \ldots, r_{\Omega}\} \)는 \( \Omega \)개의 요소를 가진 벡터이며, 각 요소 \( r_{\omega} \)는 비음수 실수입니다. \( \alpha \)가 양수일 때, 이 함수는 벡터 \( \mathbf{y} \)의 최대값을 근사하고, \( \alpha \)가 음수일 때는 최소값을 근사합니다. 또한, 이 함수의 그라디언트는 softmax 또는 softmin 함수와 동일하다는 장점이 있습니다. 이는 최적화 문제에서 중요한 성질로, 부드러운 최대/최소 함수가 필요할 때 유용합니다. 함수의 근사 오차는 다음과 같이 하한으로 제한됩니다:

\[ lse_{\alpha>0}(\mathbf{y}) \geq \max\{\mathbf{y}\} \geq lse_{\alpha>0}(\mathbf{y}) - \frac{\log(\Omega)}{\alpha} \]
이 불등식은 \( lse_{\alpha} \) 함수가 벡터 \( \mathbf{y} \)의 최대값을 \( \alpha \)가 양수일 때 얼마나 잘 근사하는지를 수치적으로 나타냅니다. 여기서 \( \Omega \)는 벡터의 길이(요소의 수), \( \log(\Omega) \)는 softmax 함수의 평활화 정도를 조절하는 항입니다. \( \alpha \)의 값이 클수록 근사 오차는 감소합니다.

 

(자세한 내용은 생략; 논문 참고)

VI. REFORMULATION OF TRAJECTORY OPTIMIZATION

이 섹션에서는 궤적 계획에서 제약 조건 식 (5c-5f)(9)의 특성을 분석하고 이를 각각 제거하기 위한 targeted approaches을 사용합니다. 그런 다음, 원래의 최적화 문제는 더 효율적으로 해결할 수 있는 unconstrained program으로 재정의됩니다.

A. Feasibility Constraints

우리는 discrete-time summation-type penalty term \( S_{\sum} \) 을 채택하여 제약 조건 식 (9)의 실행 가능성을 완화합니다.

"여기서 \( w_d \)는 다양한 종류의 제약 조건에 해당하는 패널티 가중치입니다. \([\bar{\omega_0}, \bar{\omega_1}, \ldots, \bar{\omega}_{\lambda-1}, \bar{\omega}_\lambda]\)은 사다리꼴 규칙에서 나온 quadrature coefficients \([1/2, 1, \ldots, 1, 1/2]\)입니다. 그리고 \( P_{d,i,j,k} \)는 constraint point에 대한 violation penalty입니다. 또한, 우리는 연속적인 미분 가능성과 패널티 항의 비음수성을 보장하기 위해 first-order relaxation function \( L_1(\cdot) \)를 정의합니다:"

$a_0 = 1$일 때의 $L_1(x)$의 그래프

여기서 \( a_0 = 10^{-4} \)은 경계점입니다. 이러한 이산 패널티 수식은 continuous-time constraints인 식(5g)이 허용 가능한 오차 내에서 만족됨을 보장합니다. 그런 다음, 차량의 궤적 최적화는 다음과 같이 다시 형식화됩니다:

기존 Optimization 식

 

(5g) constraint 조건이 cost로 변형된 식

trajectory의 각 constraint point에서 violation penalty의 gradient는:

 

B. Continuity Constraints

• "piece-wise polynomial의 경우, 각 부분의 연결점(waypoints $q_i$)에서 고차 연속성이 필요하여 움직임의 부드러움을 보장합니다 (식 (65d) 참조). 최적 조건 [51]을 기반으로 하면, minumum control effort piece-wise polynomial은 waypoints에서 snap-continuous해야 합니다. 따라서 piece-wise polynomial의 시작과 끝 상태가 고정된 경우, 매개변수 공간을 계수와 duration에서 waypoints와 duration으로 변환할 수 있습니다.(?) 그런 다음, 연속성 제약식 (식 (65d))을 자연스럽게 충족시킬 수 있습니다."

C. Gear Shifting Constraints

• 이전 섹션에서는 polynomial parameter space을 변환하여 최적 조건을 희생하지 않고 연속성 제약을 제거했습니다. 그러나 piece-wise polynomial의 시작 및 끝 상태는 고정되어야 합니다. 이는 GSP(Gear Shifting Point)의 상태가 고정되어야 한다는 것을 의미합니다. 그러나 GSP의 상태가 초기 추정치에 완전히 의해 결정되고 최적화에 관여하지 않는 경우, 이는 의심할 여지 없이 궤적의 자유도를 제한하고 초기 추정치에 대한 의존성을 강화하여 궤적 품질을 떨어뜨릴 수 있습니다. 따라서 이 섹션에서는 복수의 전진 및 후진 움직임이 필요한 복잡한 주행 시나리오를 더 잘 다룰 수 있도록 GSP의 상태를 더 완화하는 GSPO를 도입하여 이전 작업 [51]을 개선합니다.
• GSPO와 기어 변속 제약 제거에 대해 논의하기 전에 먼저 식(65c)을 분해하고 재구성합니다.

"기어 변속 위치인 \( p_i^g \)와 변속 전 최종 속도 \( v_i^g \)입니다. 변속 전후로 속도 방향이 바뀌고 그 크기는 최적화 중 발생할 수 있는 특이점을 방지하기 위해 작은 비제로 값 \( \bar{v} \)로 설정됩니다. 편안함을 보장하기 위해 GSP에서의 가속도는 0으로 고정되며 이후의 완화 과정에는 참여하지 않습니다. GSPO를 도입하는 핵심은 GSP에서의 상태를 궤적 표현 공간에 독립적인 자유 최적화 변수로 추가하는 것입니다. 다음 단계의 그라디언트 기반 해법을 촉진하기 위해, 우리는 \( p_i^g, v_i^g \)와 다항식 매개변수(계수와 시간) 사이의 관계 및 그라디언트 전파 체인을 유도해야 합니다. 식(67a-67c)와 섹션 VI-B에서 언급된 piece-wise polynomials의 연속성 보장을 기반으로, 우리의 독특한 궤적 표현은 본질적으로 다음과 같은 선형 방정식을 만족합니다:

여기서 \( M_i(T_i) \)는 \( \mathbb{R}^{2M_i \times 2M_i} \)에 속하는 가역적인 밴드 행렬이고, 그 구체적인 형태는 문헌 [51]에서 찾아볼 수 있습니다. \( b_{i(e1...n)} \)은 \( \mathbb{R}^{2M_i \times 2} \)에 정의됩니다."

[51] 논문에서 발췌한 $M$ matrix. $M$은 $\beta$로 이루어진 basis 이고 $c$가 piece-wise polynomial의 coefficient이다.

"연속성의 정도가 2s-1로 설정될 때 최적성 조건을 만족시키는데, GSP의 물리적 의미는 이전과 다음 piece-wise polynomials 궤적의 연결점이라는 것을 고려하면, GSP에서의 상태와 인접한 piece-wise polynomials 궤적의 그라디언트를 통해 목적 함수의 그라디언트가 전파되어야 한다는 것은 직관적입니다. 따라서 GSP에서의 상태에 대한 목적 함수의 그라디언트는 두 인접한 piece-wise polynomials 궤적의 그라디언트를 통해 전파되어야 합니다. 여기서 우리는 기어 변속 위치 \( p_i^g \)와 변속 전 최종 속도 \( v_i^g \)에 대한 그라디언트를 유도합니다:

여기서 \( e_k \)는 적절한 차원의 열 벡터로, k번째 행의 요소는 1이고 나머지는 모두 0입니다. 지금까지 우리는 성공적으로 \( p_i^g \)와 \( v_i^g \)를 궤적 표현 공간에 추가했습니다. 그런 다음 우리의 궤적 표현 공간은 경유점, 지속시간, \( p_i^g \)와 \( v_i^g \)에서 나오는 계수와 지속시간으로 진화합니다. 또한, 원래 궤적 최적화 문제는 다음과 같이 재정의됩니다:"

"여기서, 경유점 \( q \)는 \( \mathbb{R}^{2 \times \sum_{i=1}^n (M_i-1)} \)에 속하고, 기어 변속 위치 \( p^g \)는 \( \mathbb{R}^{2 \times (n-1)} \)에 속하며, 기어 변속 속도 \( v^g \)는 \( \mathbb{R}^{2 \times (n-1)} \)에 속합니다. 게다가, 제약식 Eq.(72b)를 만족시키기 위해 우리는 기어 변속 속도 \( v_i^g \)를 극좌표계에서 \( \tilde{v} \)의 \( \cos \theta_i^g \), \( \sin \theta_i^g \)로 표현합니다. 여기서 \( \theta_i^g \)의 물리적 의미는 기어 변속 전의 속도 방향입니다. 또한, 비용 함수는 \( K(q, T, p^g, v^g(\theta^g)) \)로 변환되며, 비용 함수 \( K \)에 대한 \( \theta_i^g \)의 그라디언트는 다음과 같이 얻어집니다:

이 시점에서, 마지막 등식 제약 Eq.(72b)도 제거됩니다. 요약하자면, GSPO를 도입하는 핵심 아이디어는 궤적의 매개변수 공간을 변환하고 궤적을 경유점, 지속시간, \( p_i^g \), 그리고 \( \theta_i^g \)를 사용하여 복잡한 전진-후진 운동을 가진 차량 궤적으로 최종적으로 표현하는 것입니다. 이 방법은 모든 등식 제약을 제거하면서 GSPO를 성취합니다. 또한, 우리는 궤적 품질과 효율성에 대한 GSPO의 영향을 섹션 VII-C에서 제시된 ablation 실험을 통해 평가합니다."

D. Positiveness Condition

엄격한 긍정성 조건 Eq.(72c)를 제거하기 위해, 우리는 제약이 없는 가상의 시간 \( \tau = [t_1, ..., t_n]^T \in \mathbb{R}^n \)을 정의하고, \( t_i \in \mathbb{R} \)에서 실제 지속 시간 \( T_i \in \mathbb{R}_+ \)로의 diffeomorphism map을 사용합니다:

 

그런 다음 우리는 \( \tau \)를 사용하여 실제 시간 집합 \( T \)를 대체하여 엄격한 긍정성 제약 Eq.(72c)가 자연스럽게 만족되도록 합니다. 상응하는 재구성된 최적화 문제는 다음과 같습니다:

그라디언트는 \( T_i \)에서 \( t_i \)로 전파될 수 있습니다:

요약하자면, 우리는 모든 제약을 제거하고 그라디언트를 해석적으로 유도했습니다. 마지막으로, 우리는 quasi-Newton 방법을 통해 변형된 비제약 최적화 문제를 강건하게 풉니다.

목적함수 변화과정 정리

 

---

Experiments 정리

• 제안된 방법은 시뮬레이션 및 현실 세계에서 평가되었습니다. 벤치마크 결과 우리의 플래너가 시간 효율성과 궤적 품질 측면에서 최첨단 기법을 능가하는 것을 보여줍니다. 상세한 구현에서는 전방 및 후진 기어 전환 시 속도 크기를 0.05m/s( v̄ = 0.05 m/s)로 고정함으로써 특이점을 회피했습니다. 이러한 처리로 인해 속도가 갑자기 변하는 것은 있지만, 그 정도가 제어에 미치는 부정적 영향은 무시할 정도로 미미합니다. 그 후의 추적 오차 비교 실험과 물리적 실험도 우리의 계획된 궤적의 동적 실행 가능성을 검증합니다.

A. Benchmarks

1) Configurations

• 모든 시뮬레이션 실험은 Intel Core i7-10700 CPU와 GeForce RTX 2060 GPU가 탑재된 Ubuntu 18.04에서 실행되는 데스크탑 컴퓨터에서 수행되었습니다. 물리 시뮬레이터 CARLA [54]를 기반으로 시뮬레이션 실험을 진행했습니다. 제안된 방법은 OBTPAP [33], DL-IAPS+PJSO [28], H-OBCA [31], Timed Elastic Bands (TEB) [55]와 같은 정적 비구조적 환경에서 차량 형태의 로봇의 모션 플래닝을 위해 특별히 설계된 네 가지 인상적인 방법과 비교되었습니다. 모든 방법은 자전거 모델을 사용하며 C++14로 구현되었으며 병렬 가속화를 사용하지 않았습니다. OBTPAP [33] 및 H-OBCA [31]는 이중초점 내부점 방법인 IPOPT [56]로 해결되었습니다. DL-IAPS+PJSO [28]는 OSQP [57]를 사용하여 구현되었습니다. TEB [55]에는 그래프 최적화 솔버인 G2o [58]가 사용되었습니다. 또한 공정한 비교를 위해 모든 플래너는 초기 근사값을 제공하기 위해 hybridA* [29] 알고리즘을 사용했습니다. 또한, 제안된 플래너, OBTPAP [33], DL-IAPS+PJSO [28] 및 TEB [55]는 환경의 알려진 전역 포인트 클라우드를 사용하여 충돌 방지 제약 조건을 설정합니다. H-OBCA [31]는 장애물로부터 수동으로 추출된 알려진 볼록 다각형을 사용하여 최적화 공식을 구성합니다. 수렴 조건, 동적 제약 조건, 그리고 기타 공통 매개변수는 모든 실험에서 동일하게 사용되었습니다.

2) Quantitative Results

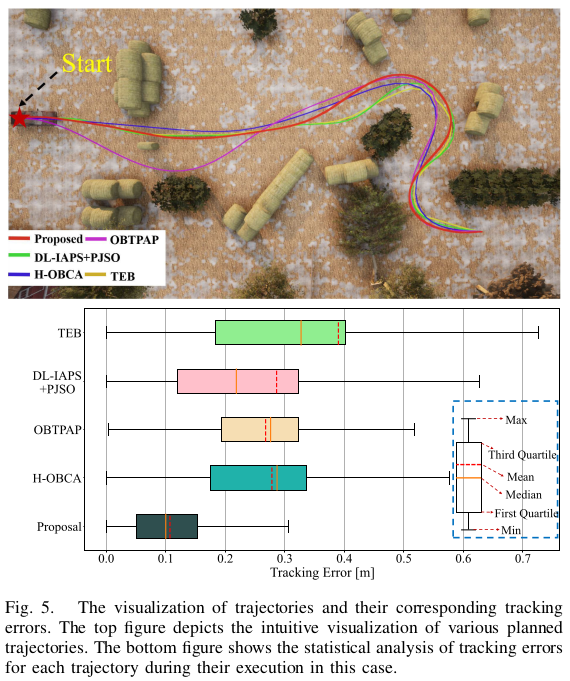
• 우리는 다양한 환경 장애물의 수와 시작-끝 거리(문제 규모로 표시됨)가 다른 여러 경우에서 광범위한 정량적 평가를 수행합니다. 각 경우에서는 무작위 시작 및 종료 상태로 여러 가지 비교 테스트를 수행합니다. 궤적의 실행 성능을 평가하기 위해 MPC 컨트롤러 [59]를 사용하여 계획된 궤적을 추적하고 추적 오차를 측정하는 위치 및 속도 오차를 최소화합니다. 더 직관적인 이해를 위해 한 실험에서 계획된 궤적과 해당 추적 오차를 도식화하였습니다(그림 5 참조). 각 실험에서 계획된 궤적의 물리적 동역학 데이터인 평균 가속도 (M.A.), jerk (M.JK), 추적 오차 (M.TE)를 기록하였습니다 (표 I 참조). 또한 각 경우의 평균 계획 시간을 계산하고 이를 로그 히스토그램으로 도식화하였습니다(그림 6 참조). 시뮬레이션 결과를 기반으로, 우리의 방법은 궤적 실행 성능, 움직임 편안함 및 시간 효율성 측면에서 다른 방법들보다 상당한 장점을 가지고 있다고 판단됩니다. 1) 추적 오차 측면에서, 그림 5와 표 I은 우리의 계획된 궤적이 최소 추적 오차를 나타내어 하위 컨트롤러에 의해 실행될 때 우수한 실행 성능을 보인다는 것을 보여줍니다. 이는 우리 궤적의 강력한 공간-시간 최적 변형 능력과 효과적인 고차 연속 궤적 표현에 기인합니다. 이산적인 모션 프로세스를 사용하는 방법과 비교하여, 우리의 접근 방식은 상태 및 유한 차원 도함수의 연속성을 본질적으로 보장하여 우리의 궤적을 실제 물리적 모션 프로세스에 더 가깝게 만들어 실행하기 쉽게 합니다. 2) 동적 메트릭 측면에서, 표 I은 우리의 궤적이 낮은 가속도와 제르크를 나타내어 더 나은 인간 편안함을 제공한다는 것을 보여줍니다 [44]. 3) 시간 효율성 측면에서, 그림 1의 히스토그램은 우리의 알고리즘이 각각의 경우에서 다른 알고리즘에 비해 한 차원 더 높은 효율성을 보인다는 것을 보여줍니다. 특히 대규모 궤적 생성 문제에서 두드러지게 나타납니다. 더불어 결과는 우리의 방법이 문제 규모와 환경 장애물의 수에 대한 강건성을 보여주며 다양한 시나리오에 적응할 수 있다는 것을 보여줍니다. H-OBCA [31]가 장애물과의 거리를 정확하게 인코딩하기 위해 듀얼 변수를 직접 도입한다는 점에서 고품질의 궤적을 생성할 수 있습니다. 그러나 시간 효율성과 강건성 측면에서 우리의 방법이 H-OBCA [31]를 능가한다고 판단됩니다. 그 이유는 계산 부담이 많아 적용하기 어려워지기 때문입니다. (이 논문의 장점)

B. Dynamic Obstacle Avoidance

• 우리는 제안된 플래너를 210m × 50m의 동적인 비구조화된 환경에서도 검증했습니다. 이 환경에서는 자율 주행 차량이 정적 장애물과 여덟 대의 다른 차량으로 이루어진 교통 흐름을 피해야 했습니다(그림 7 참조). 이 논문에서는 인지에 중점을 두지 않기 때문에, 환경과 다른 차량의 궤적은 플래너에게 알려진 상태입니다. 모든 차량의 최대 속도는 10m/s로 설정되어 있습니다. 그림 7의 차량과 궤적의 색깔은 움직임 타임스탬프를 나타내며, 이는 자율 주행 차량과 다른 이동 물체 간의 공간적 및 시간적 교차점이 없음을 나타냅니다. 이는 동적인 충돌 없음을 시연하고 있습니다. 객체들의 전체 차원 모델링 덕분에, 자율 주행 차량은 좁은 영역을 통과하는 안전 공간을 완전히 활용할 수 있습니다. 특히 확대된 부분에서 확인할 수 있습니다. 자율 주행 차량의 궤적 길이는 260m이며, 계산 시간은 단 0.18초로, 특히 긴 거리의 글로벌 궤적 생성에 대한 우리 플래너의 효율성을 시연하고 있습니다.

C. Ablation Experiments

D. Real-World Experiments

• 추가적으로 시뮬레이션 외에도 실제 물리적 플랫폼에서 우리의 플래너의 실행 가능성을 검증하기 위해 실제 실험도 진행합니다. 실험 지역은 그림 9에 나타난 것처럼 밀집한 40m × 20m의 야외 비구조화 주차장입니다. 움직이는 로봇은 초기 상태에서 시작하여 장애물을 피해 이동한 후, 사람이 정의한 헤딩 각도로 주차 공간으로 후진해야 합니다. 전체 트랙의 길이는 약 42m입니다. 실제 세계 실험은 SAIC-GM-Wuling Automobile Baojun E300 2에서 진행되었으며, 이 차량의 크기는 2.9m × 1.7m × 1.6m이며 휠베이스는 2m이며 GPS가 없습니다. 동시에, 실시간 위치 파악, 제어 및 데이터 기록을 위해 한 개의 스테레오 카메라, 네 개의 피시아이 카메라 및 열두 개의 초음파 센서가 플랫폼에 배치되어 있습니다. 또한, 실제 세계 실험에서는 높은 정밀도의 LIDAR나 정확한 외부 위치 결정 시스템을 사용하지 않았습니다. 모든 모듈은 C++로 구현되어 있으며 QNX 운영 체제로 구성된 TI TDA4 칩(64-bit Dual Arm Cortex-A72 @2000MHz) 3에 배포되었습니다. 플래닝 중에는 차량 형태가 0.25m 확장되어 현실적인 실행 시 피할 수 없는 제어 및 위치 오류가 있더라도 충돌 없음을 보장했습니다. 전진 및 후진 최대 속도는 각각 2m/s 및 0.5m/s로 설정되었습니다. 시간 가중치 $w_T$는 경로의 공격성을 보장하기 위해 50으로 설정되었습니다. 그림 11에서 보이는 것처럼, 자율 주행 차량은 계획된 경로를 따라 장애물을 피하고 사용자가 지정한 헤딩 각도로 주차 공간으로 후진할 수 있음을 시각화했습니다. 더 나아가 동적 평가 지표는 Tab. III에서 양적으로 측정되었습니다. 우리는 차량이 동적 한계를 초과하지 않으면서도 목표 상태에 도달하기 위해 상대적으로 높은 속도를 유지하면서도 승객의 편안함을 보장하기 위해 낮은 제르크를 유지하는 것으로 확인됩니다. 마지막으로 보충 자료에서 더 많은 시연을 찾을 수 있습니다.

ATTACHMENTS

• 저희는 불확실성이 자율 주행에 미치는 영향을 평가하기 위해 50m × 10m의 알려지지 않은 환경에서 시뮬레이션 실험을 수행합니다. 그림 12에 나타난 것처럼, 차원이 0.8m × 0.5m인 로봇은 최대 10m까지 감지할 수 있는 Omni-directional Radar로 장착되어 있습니다. 플래너가 궤적을 출력한 후에는 MPC 기반 컨트롤러를 사용하여 이를 따릅니다. 이 실험에서 사용되는 노이즈 $n$을 가진 운동 모델은 다음과 같습니다:

• 여기서 $[ p_x , p_y ]$는 후방 중심의 위치이고, v는 경도 속도, φ는 조향 각도, θ는 요 휘도, a는 경도 가속도, ω는 조향 각 속도이며, $L_w$는 휠베이스입니다. 여기서 노이즈와 함께 정의된 상태 전이 방정식 $f$는 다음과 같습니다:

• $q$는 이론적인 상태 전이이고, $N = nq$는 운동의 변화에 비례하여 정의된 불확실성 항입니다. 여기서 $n$은 각 요소가 $[h_1, h_2]$에서 균일한 분포를 따르는 무작위 노이즈의 강도를 나타내는 대각 행렬입니다. 이 실험에서는 다음 두 조건 중 하나가 충족되면 재계획이 트리거됩니다: 1) 초기 궤적이 새로 감지된 장애물과 충돌하거나 2) 추적 오차가 0.1m를 초과합니다. 두 번째 조건으로 트리거된 재계획의 횟수를 R.N으로 표시합니다. 실제 시나리오를 더 잘 모사하기 위해 이 실험에서는 컨트롤러와 액추에이터 사이에 지연을 도입했습니다. 실험 케이스는 노이즈와 지연의 수준을 기준으로 네 가지 그룹으로 분류됩니다: 자유 불확실성, 낮은 불확실성, 중간 불확실성 및 높은 불확실성. 각 케이스에 대해 R.N, 평균 추적 오차 (M.TE), 궤적 길이 (T.L), 평균 가속도 (M.A), 평균 조향 각 속도 (M.SR)를 계산합니다. 이러한 결과는 불확실성의 증가가 세 가지 부정적인 영향을 불러옴을 보여줍니다: 1) 증가한 추적 오차는 궤적 실행의 어려움을 나타내며, 2) 증가한 평균 가속도와 조향 속도는 더 높은 제어 노력을 시사하며, 3) 더 긴 궤적은 더 많은 곡선 운동과 최적성 감소를 의미합니다. 불확실성이 존재함에도 불구하고, 로봇은 고주파 컨트롤러 피드백 및 실시간 재계획 능력 덕분에 미지의 환경에서 안전하게 탐색합니다. 또한, Tab. IV에 제시된 결과는 불확실성의 증가가 과도한 추적 오차로 인한 재계획 횟수의 증가로 이어진다는 것을 보여줍니다. 빠른 재계획 메커니즘을 통해 로봇은 궤적 이탈을 수정하고 누적된 추적 오차를 제거하여 불확실성에 대한 견고성을 향상시킵니다. 물론, 잠재적인 불확실성을 컨트롤러에 통합함으로써 시스템 전반적인 불확실성에 대한 저항성을 향상시킬 수 있다는 점을 인정합니다. 또한, 계획 단계에서 불확실성을 고려함으로써 궤적을 추적하기 쉬워질 수 있다는 점을 앞으로의 연구에서 다룰 예정입니다.

---

CONCLUSION

• 이 논문에서는 미분 평탄성 특성을 기반으로 한 효율적인 공간-시간 최적 계획 시스템을 제안합니다. 우리의 방법은 여러 가지 주요 기능을 갖추고 있습니다. 첫째, 우리의 궤적 표현은 본질적으로 고차 연속성을 가지며 운동 과정을 이산화하지 않아 실제 운동 과정을 더 잘 근사할 수 있습니다. 둘째, point mass models는 달리 장애물 회피를 위해 볼록 근사화를 구현하여 해결 공간을 충분히 활용합니다. 셋째, 초기 값에 대한 강건성을 높이기 위해 원래의 최적화 문제를 완화하고 기어 전환 지점에 상태 최적화를 도입합니다. 우리의 방법은 효율성과 궤적 품질 사이에 좋은 균형을 이루며, 시뮬레이션 실험에서 우리의 방법이 가장 높은 효율성을 유지하면서도 가장 낮은 추적 오차를 보이는 것으로 나타났습니다. 이는 우리가 생성한 궤적이 하위 수준 컨트롤러에 의해 잘 실행될 만큼 충분히 부드럽다는 것을 의미합니다. 실제 세계에서의 실험은 또한 우리의 방법이 실제 플랫폼에서의 효과를 검증합니다. 앞으로는 우리의 방법을 다중 로봇에 확장하고 다른 운동 모델에 적용 가능성을 탐구할 계획입니다. 더 나아가, 우리는 등산 및 하산 궤적과 같은 도전적인 지형에 대한 운동 계획에 노력을 기울일 것입니다. 우리의 궁극적인 목표는 다양한 로봇 플랫폼과 환경에 적용할 수 있는 포괄적인 운동 계획 프레임워크를 개발하는 것입니다.