- Youtube (FAST-Lab): https://www.youtube.com/watch?v=qdYr3BKHsdM
- Github (FAST-Lab): https://github.com/ZJU-FAST-Lab/Car-like-Robotic-swarm?tab=readme-ov-file
GitHub - ZJU-FAST-Lab/Car-like-Robotic-swarm: Source code for the decentralized car-like robotic swarm
Source code for the decentralized car-like robotic swarm - GitHub - ZJU-FAST-Lab/Car-like-Robotic-swarm: Source code for the decentralized car-like robotic swarm
github.com
Abstract 정리
- 이 논문에서 우리는 혼잡한 환경에서 실시간 계획이 가능한 차량과 같은 로봇 군집을 위한 decentralized frame-work를 제안합니다. 이 시스템에서는 경로 탐색이 환경의 위상 정보에 의해 안내되어 자주 변하는 위상을 피하고, 검색 기반의 속도 계획을 사용하여 실행 불가능한 초기 값의 국소 최소값에서 벗어납니다. 그런 다음 공간-시간 최적화를 사용하여 안전하고 부드럽고 동적으로 실행 가능한 궤적을 생성합니다. 최적화하는 동안 궤적은 고정된 시간 단계로 이산화됩니다. 에이전트 간의 signed distance에 대한 벌칙을 부과하여 충돌 회피를 실현하고, 차량의 전방 조향각 제한과 함께 differential flatness가 비홀로노믹 제약 조건을 만족합니다. 궤적이 무선 네트워크로 방송됨에 따라, 에이전트들은 잠재적인 충돌을 확인하고 방지할 수 있습니다. 우리는 시뮬레이션과 실제 실험에서 우리 시스템의 강인함을 검증합니다. 코드는 오픈 소스 패키지로 공개될 예정입니다.
Introduction 정리

- 이 논문에서는 다중 로봇 시스템이 작업 완료를 크게 가속화할 수 있는 유연성과 안정성으로부터 혜택을 받는다고 설명합니다. 현재, 차량과 같은 로봇 군집은 실생활에서 널리 사용되고 있으며, 예를 들어 항구의 자율 트럭, 물류 창고의 자동 유도 차량, 위험한 상황에서의 수색 및 구조, 미지의 환경 탐사 등에 사용됩니다. 이러한 시스템 대부분은 중앙집중식 계획 프레임워크에 의존하고 있습니다. 하지만 로봇의 양과 지도의 복잡성이 증가함에 따라 중앙집중식 방법은 높은 계산 부담을 겪고 있으며, 이로 인해 동적 환경에 적응하는 능력이 부족하여 차량과 같은 로봇 군집의 실용적 사용을 제한합니다. 분산 방법에서는 계산 부담이 각 에이전트에 의해 분리되지만, 온보드 프로세서의 성능에 제한되어 궤적의 품질이 보장되지 않을 수 있습니다. 이러한 격차를 메우기 위해, 우리는 장애물이 많은 환경에서 실시간 계획이 가능한 차량과 같은 로봇 군집을 위한 분산 계획 프레임워크를 제안합니다.
차량과 같은 로봇은 쿼드로터와 같은 홀로노믹 운동학을 가진 로둣와는 달리, 혼잡한 환경에서 실시간 계획을 위한 더 많은 도전을 제시합니다. 항해하는 동안, 정적 및 동적 장애물과의 충돌을 피하기 위해 자주 재계획을 수행해야 합니다. 비홀로노믹 운동학으로 인해, 궤적의 위상 구조에서 급격한 변화에 적응하는 것이 차량과 같은 로봇에게는 더 어렵고, 이는 특히 에이전트가 장애물에 가까울 때 정적 장애물과 충돌할 확률이 높아지는 결과를 가져옵니다. 이러한 어려움을 극복하기 위해, 우리는 topology-guided path planning을 도입하여 궤적 일관성을 보장하며, 이는 재계획된 경로가 마지막으로 계획된 것과 위상 호모토피를 유지함을 의미합니다.
back-end optimization에서, 초기 값은 중요한 역할을 합니다. 실행 가능한 초기 값은 최적화 수렴을 가속화하고 나쁜 해의 국소 최소값에 빠지는 것을 피하는 이점을 가져오지만, 실행 불가능한 초기 시간 배치는 다른 에이전트와 충돌하는 궤적으로 수렴할 수 있는 해에 이르게 할 수 있습니다. 합리적인 초기 시간 할당을 얻기 위해, 우리는 검색 기반의 속도 계획을 도입합니다. 위상-유도 경로 계획에 의해 공간적 경로가 결정되면, 속도 계획은 다른 에이전트와의 충돌 회피뿐만 아니라 동적 실행 가능성을 실현하는 시간 범위를 생성합니다.
공간적 및 시간적 초기 값을 기반으로, 우리는 공간-시간 합동 최적화를 사용하여 차량과 같은 로봇의 비홀로노믹 제약 조건을 만족하는 부드럽고 안전하며 실행 가능한 궤적을 생성합니다. 제안된 시스템은 단일 차량 운동 계획에 중점을 둔 이전 작업[1]의 확장 및 수정입니다. 위상-유도 경로 계획 및 속도 계획에 더하여, 우리는 특히 다중 에이전트 임무에 대한 계산 효율성을 더욱 향상시키기 위해 고정된 시간 단계 궤적 이산화 전략을 채택합니다. 이 시스템에서, 궤적은 통신 모듈에 의해 방송되며, 이는 다른 에이전트가 실시간 계획을 수행하는 데 사용됩니다. 전체 군집 시스템은 에이전트 간의 충돌 없이 미지의 환경을 통과할 수 있습니다.
우리는 차량용 고정밀 시뮬레이션 플랫폼과 실제 실험에서 우리 시스템의 강인함을 검증합니다. 이 군집의 각 에이전트는 온라인 센싱, 매핑, 계획 및 제어를 독립적으로 수행하며, 궤적은 서로에게 방송됩니다. 이 논문의 기여도는 아래와 같이 요약됩니다:
1) 로봇의 motion consistency을 개선하기 위해 topology-guided path planning을 도입하고, back-end optimization를 위한 실행 가능한 초기 값을 제공하기 위해 검색 기반의 속도 계획을 활용합니다.
2) 고정된 시간 단계로 궤적 이산화 전략을 수정하여 궤적 최적화 과정의 계산 효율성을 향상시킵니다.
3) 경로 계획, 속도 계획 및 공간-시간 최적화를 결합하고, 분산 차량과 같은 로봇 군집을 구현하여 혼잡한 환경에서 실시간 실행을 실현합니다.
4) 연구 커뮤니티에 제공하기 위해 우리의 코드를 오픈 소스 패키지로 공개할 예정입니다.
Related Works 정리
A. Trajectory Optimization for Car-Like Robots
- 동역학 모델의 복잡성은 차량과 같은 로봇에 대한 계획 수립에 어려움을 가져오며, 최적화 기반 방법은 실행 가능한 궤적을 생성하기 위해 깊이 탐구되었습니다. Zhu et al. [3]은 초기 비볼록 문제를 이차 목적 및 이차 제약조건을 가진 볼록 최적화로 변환합니다. Zhou et al. [4]은 곡률 제약을 완화하기 위해 순차적 볼록 최적화를 사용합니다. Zhang et al. [5]은 최적화 기반 충돌 회피 알고리즘을 제안합니다. Li et al. [6]은 간소화된 차량 모델을 안전 회랑 내에서 제약함으로써 충돌 회피를 실현합니다. 그러나 위의 방법들은 여전히 복잡한 수학적 모델로 인해 낮은 계산 효율성 (기존 방법들의 단점) 을 겪고 있습니다. 최근에는 차량을 위한 차동 평탄성 기반 궤적 계획 프레임워크 [1]가 제안되어 복잡한 환경에서 빠른 계산을 달성했습니다. 위의 기초 [1]에 기반하여, 우리는 다중 로봇 시나리오에서 계산 부담을 더욱 줄이기 위해 궤적 이산화 전략을 수정 (기존 방법론에서 효율성 개선)했습니다.
B. Car-like Robotic Swarm in Cluttered Environments
- 차량과 같은 로봇 군집은 중앙집중식 및 분산식 프레임워크로 나눌 수 있습니다. Mora et al. [7], [8]은 RVO(Reciprocal Velocity Obstacles) 및 ORCA(Optimal Reciprocal Collision Avoidance)를 기반으로 충돌 회피를 실현하고, 그 후에 부드러운 궤적을 생성하기 위해 최적화 과정을 사용합니다. Li et al. [9], [10]은 두 단계에서 시간 최적 MVTP(Multi-Vehicle Trajectory Planning) 문제를 해결하고 밀집된 환경에서 군집 계획을 달성합니다. 위의 프레임워크들은 중앙집중식 방법을 기반으로 하지만, 로봇 수가 증가함에 따라 중앙집중식 방법은 계산 복잡성에 의해 제한 (centralized 방법의 단점)을 받습니다. Delimpaltadaki et al. [11]은 전임자-추종 제어 문제를 해결하기 위해 분산식 프레임워크를 제안합니다. 그러나 이 연구 [11]는 교차로와 같은 복잡한 작업에 적응할 수 없는 플래툰 시나리오에 한정되어 있습니다. 이 논문에서는 차량과 같은 로봇 군집을 구축하기 위해 분산식 계획 프레임워크를 채택합니다.
C. Topology-Guided Path Planning
- 위상 계획은 최상의 공간적 경로를 선택하고 국소 최소값을 피하기 위해 많은 시나리오에서 적용되었습니다. Jaillet et al. [12]은 위상 호모토피를 정의하고 환경의 위상 정보를 인코딩하기 위해 visibility deformation 로드맵을 구축합니다. Zhou et al. [13], [14]은 위상적 동등성을 확인하여 실시간 계획을 제안하기 위해 가시성 변형을 확장합니다. Zhou et al. [15]은 장애물의 다양한 방향에서 거리 필드를 구축하고 가시성 변형을 사용하여 독특한 궤적을 찾습니다. 이 논문에서는 작업 [12], [13]의 visibility deformation을 더 넓은 정의로 확장하여 마지막으로 계획된 경로와 path homeomorphic (동형 경로)를 탐색합니다.
D. Speed Planning
- 공간-시간 분해는 자율 주행에서 계획 효율성을 향상시키기 위해 널리 사용되는 전략이며, 여기에서 속도 계획은 시간적 부분입니다. 작업 [16], [17]은 실행 가능한 속도 프로파일을 검색하기 위해 검색 기반의 속도 계획을 사용합니다. 작업 [18], [19]은 부드러운 S-T(Space-Time) 곡선을 생성하기 위해 최적화 기반의 속도 계획 방법을 제안합니다. Johnson et al. [20], [21]은 도달 가능한 속도 세트를 전파하여 동적 장애물 회피를 실현합니다. 다른 작업들 [22], [23]은 베지에 다항식을 최적화하여 속도 계획을 수행합니다. 그러나 대부분의 기존 방법은 공간-시간 합동 최적화 없이 부드럽고 실행 가능한 속도 프로파일을 얻는 데 중점 (PVD 방법의 단점)을 둡니다. 이 논문에서는 공간-시간 계획을 분리하며, 초기 시간 범위는 검색 기반의 속도 계획에 의해 제공됩니다. 그런 다음 초기 경로는 이후 refined by subsequent spatial-temporal optimization. 따라서 초기 시간 범위는 기존 방법이 요구하는 것처럼 부드럽거나 정확할 필요가 없습니다.
Methodology 정리
3. Path and Speed Planning
이 절에서는 위상-유도 경로 계획과 검색 기반 속도 계획에 대해 소개하고 있으며, 이들은 back-end optimization를 위한 공간적 및 시간적 초기 값으로 사용됩니다.
A. Topology-Guided Path Planning
최적화 이전에 공간 참조 경로를 생성하기 위해, 우리는 차량 사례에서 Kinodynamic 하이브리드 A* [24]를 채택합니다. 다양한 자세를 샘플링하는 대신, 우리는 직접 다양한 조향 각도를 샘플링하며, 각 운동 기본 요소는 동일한 경도 거리를 공유합니다. 최대 조향 각도를 제한함으로써 비홀로노믹 제약 조건이 처음부터 만족될 수 있습니다.
Topological homotopy 개념은 [12], [13]에서 분석되었으며, 이는 다양한 위상 구조를 가진 후보 궤적을 포착하는 것을 목표로 합니다. 그러나 [12]의 가시성 변형(VD)과 [13]의 균일 가시성 변형(UVD)은 후보 궤적이 동일한 시작점과 종료점을 공유해야 한다고 요구 (기존 방법론의 단점)합니다. 우리의 검색 과정에서, 재계획 시작점은 이전에 검색된 경로에 위치하지 않을 수 있으므로, 우리는 VD를 SD-VD로 아래와 같이 더 넓은 정의로 확장 (이 논문에서 개선한 부분)합니다:
정의 1: SD-VD 조건: pre-defined distances S, D ∈ R+에 대해, 두 궤적 τ1(s), τ2(s) : R → R2 parameterized by arc length s ≥ 0, 모든 s ≤ S에 대해, line τ1(s) - τ2(s)가 collision-free, ||τ1(s) - τ2(s)||2 ≤ D인 경우 동일한 SD-VD 클래스에 속합니다.


우리는 SD-VD를 경로 확장 과정에 도입하여 마지막으로 계획된 경로와 동형(homeomorphic)의 운동학적 경로를 얻습니다. 경로 확장 전에, 이전 운동학적 경로는 호 길이 s에서 τ0 경로의 위치를 나타내는
SD-VD 및 검색 과정은 그림 4에 표시됩니다. 거리 S 및 D는 센싱 범위 및 로봇의 운동학적 특성에 기반하여 선택되며, 이는 로봇이 장애물과 충돌하지 않고 조향 각도를 조정할 수 있는 충분한 공간이 있음을 요구합니다. 그 결과, 검색된 경로는 마지막으로 계획된 경로와 동일한 위상 호모토피에 위치하며, 궤적 일관성을 보장하고 충돌을 피합니다.
B. Search-base Speed Planning
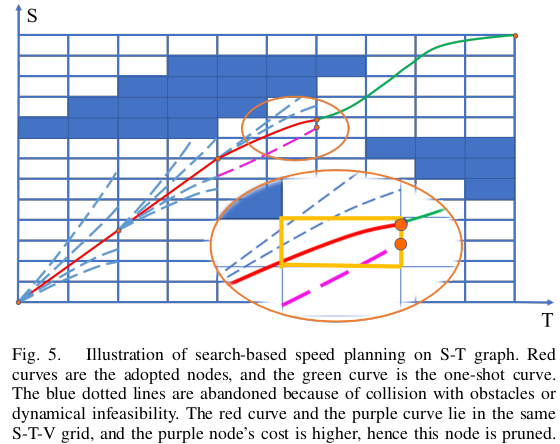
III-A에서 생성된 공간적 경로와 다른 에이전트들로부터 방송된 궤적을 기반으로, 속도 계획 전에 S-T(공간-시간) 그래프가 구성됩니다. [17]에서 수행된 것처럼, 호 길이 공간 S와 시간 공간 T를 격자로 이산화하고, S-T 공간의 점들을 반복하여 자기 로봇이 다른 에이전트와 충돌하는지 확인합니다. 충돌하는 경우, S-T 그래프의 해당 격자는 충돌 영역으로 표시되며, 이는 속도 계획에서 이 영역이 접근 불가능함을 의미합니다.
속도 계획은 동적 장애물 회피 및 운동학적 실행 가능성을 만족하는 시간 범위를 생성합니다. 우리는 [16]과 유사한 검색 기반 속도 계획 방법을 채택하고 S-T 그래프에서 1차원 A* 검색을 수행합니다. 제어 입력은 접선 가속도 A = {a min ≤ a 1 , . . . , a k ≤ a max }로 설정되며, 각 자식 노드는 동일한 시간 간격 T f 를 공유합니다. 초기 상태
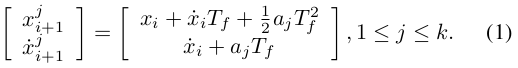
검색 과정 중에, 동적 제약을 위반하거나 충돌 영역에 도달하는 모든 노드는 버려집니다. 각 노드의 비용은 다음과 같이 정의됩니다:

여기서
1) node pruning mechanism: S-T 그래프 구축에서, 우리는 S 공간과 T 공간을 이산화합니다. 이를 기반으로, 우리는 속도 공간 이산화를 추가하여 각 노드 상태가 S-T-V 이산화 격자에 속하도록 합니다. 새롭게 확장된 노드가 이전에 확장된 노드와 동일한 S-T-V 격자에 떨어지면, 우리는 더 낮은 비용 J p 를 가진 노드만 보존하고, 다른 노드는 가지치기합니다. 그림 5에서 보여지듯이, S-T-V 공간 이산화를 제한함으로써 중복 노드의 수를 현저히 줄일 수 있습니다.
2) One-shot machanism: 각 확장된 노드에 접근할 때, 현재 상태에서 종료 상태까지 bang-bang control [25]를 수행합니다. S-T 그래프에서 bang-bang control curve이 충돌 영역과 교차하지 않으면, 검색 과정이 종료되고 해당 노드는 속도 계획의 최종 결과로 사용됩니다. 원샷 메커니즘을 적용함으로써, 검색 과정은 조기에 완료될 수 있으며, 이는 실시간 성능을 보장합니다.
4. Spatial-Temporal Optimization
이 절에서는 궤적 표현 및 최적화 공식을 소개합니다. 비용 함수를 계산하기 위해 fixed time discretization strategy하며, 이를 통해 계산 부담이 더욱 완화됩니다. 비홀로노믹 제약 조건을 만족시키기 위해, 차동 평탄성의 수학적 편차와 전방 조향 각도에 대한 제약 조건이 도입됩니다. 그 후, 군집 시나리오에서 에이전트 간의 충돌 회피 공식화를 소개합니다. 그 이후에 채택된 궤적 이산화 전략의 장점에 대해 논의합니다.
A. Trajectory and Optimization Formulation
Cartesian coordinate에서 간소화된 운동학 자전거 모델에 대한 차동 평탄성 특성을 활용하여 네 바퀴 차량을 설명합니다. [26]에서 설명한 바와 같이, 차량과 같은 로봇의 상태는 평탄한 출력
궤적은
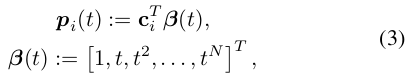
where t ∈ [0, δT ], and i ∈ {1, 2, ..., M }.
최적화 공식화를 소개하기 전에, 먼저 위반 함수
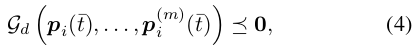
여기서 t̄는 이 조각에서 어떤 제약점의 상대적 타임스탬프입니다.
[27]에서 증명된 바에 따르면, Eq.(4)의 부등식 제약 조건은 패널티 항
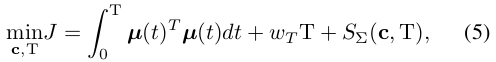
여기서
궤적은 고정된 시간 단계에 의해 여러 제약점으로 이산화됩니다. 각 시간 단계는 δt = 0.2s이며, 총 제약점의 수는 K = ⌊T/δt⌋입니다. 부등식 제약 조건을 만족시키기 위해, 모든 제약점에 패널티를 부과하고 시간에 대해 위반 함수를 적분하여 패널티 항을 얻습니다. 패널티의 표현은 다음과 같습니다:
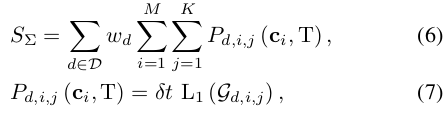
여기서

연쇄 규칙에 따라, J에 대한
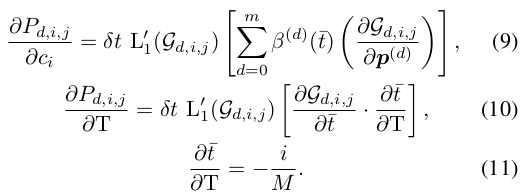
B. Front Steer Angle Limitation
차량과 같은 로봇의 비홀로노믹 제약 조건은 전방 조향 각도 제한과 관련이 있습니다. 차동 평탄성 모델에 따르면, 조향 각도 ϕ는 평탄한 출력에 의해 표현될 수 있습니다:
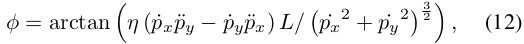
여기서 η ∈ {−1, 1}는 차량이 전진하거나 후진하는 것을 나타냅니다. L은 휠베이스 길이입니다. 그런 다음 곡률 C는 다음과 같습니다:
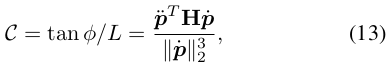
최대곡률
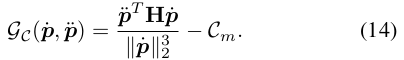
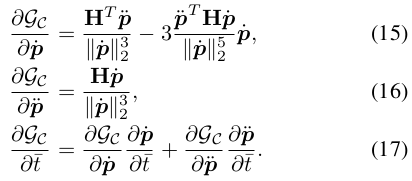
C. Collision Avoidance between Agents
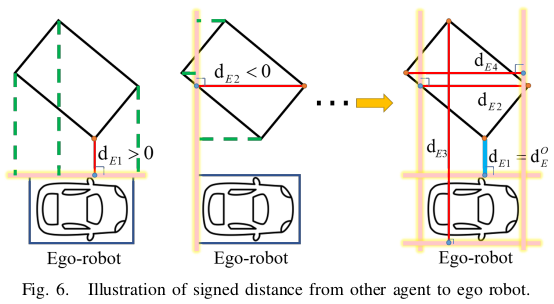
이 시스템에서 각 에이전트는 convex polygon으로 모델링됩니다. 최적화 과정에서, 동적 장애물 충돌 회피는 볼록 다각형 간 각 제약점에서 서명된 거리를 계산하여 충족시키며, 거리가 짧을 경우 패널티가 부과됩니다.
자기 차량(ego car)과 장애물 다각형의 꼭짓점 수를 각각
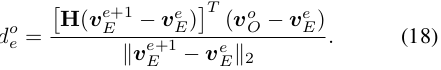
자기 차량의 e번째 모서리에 대해, 장애물의 모든 꼭짓점을 반복하여 최소 거리를 찾습니다:
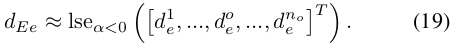
그런 다음
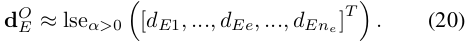
마찬가지로, 자기 차량에서 장애물까지의 signed distance는
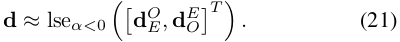
서명된 거리는 그림 6에 표시됩니다.
위의 서명된 거리를 기반으로, 충돌
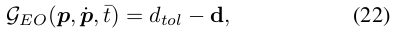
여기서
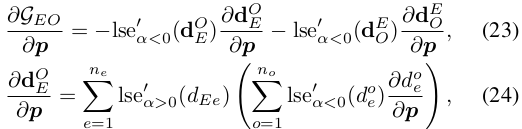
마찬가지로,
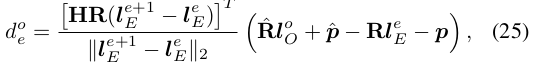
여기서 R̂ 과 p̂ 는 각각 장애물의 회전 행렬과 위치를 나타냅니다. 이 식에서 R은 p, ṗ 및 t̄와 관련이 있습니다. 따라서
D. Discussion
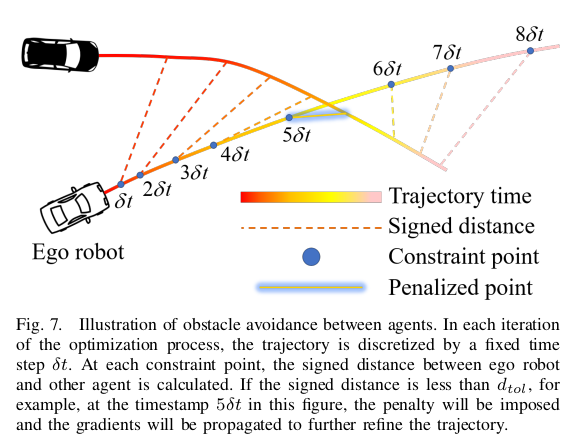
- 여기에서는 고정 시간 단계 이산화 전략의 장점에 대해 논의합니다. 이전 작업 [1]에서는 궤적의 각 조각이 고정된 수의 구속점에 의해 균일하게 이산화되었습니다. 최적화 프로세스가 반복되면서 제약 지점의 위치와 타임스탬프가 변경됩니다 ([1] 의 단점). 각 제한점의 순간에 동적 장애물의 상태를 획득하기 위해 제한점의 절대 타임스탬프를 의미하는 t̂를 도입합니다. 직관적으로 t̄는 자아 로봇의 상태를 계산하는 데 사용되는 반면, t̂는 전달된 궤적을 통해 다른 에이전트의 상태를 색인화하고 계산하는 데 사용됩니다 ([1]의 단점을 해결하기 위한 해결책). t̄와 t̂ 모두 궤적 T의 총 지속 시간과 연관되어 있습니다. Eq.(25)에서 변수 R̂ 및 p̂는 절대 타임스탬프 t̂와 관련이 있습니다. 이전 연구에서 위반 함수는 GEO(p, ṗ, t̄, t̂)로 정의되었습니다. ∂G EO /∂ t̂를 얻으려면 기울기 ∂ R̂/∂ t̂ 및 ∂ p̂/∂ t̂도 고려하고 계산해야 합니다. 본 논문에서는 고정된 시간 간격으로 궤적을 이산화합니다. 이는 제약 지점의 타임스탬프가 최적화 반복에 따라 변하지 않는다는 것을 의미합니다. 따라서 각 제약점에 해당하는 다른 에이전트 R̂, p̂의 상태는 고정되어 있어 추가 변수 t̂ 및 관련 계산을 생략할 수 있음을 나타냅니다. 또한, 궤적이 최적화되기 전에 상태 R̂ 및 p̂를 미리 계산하여 목록에 저장할 수 있습니다. 따라서 최적화 반복 중에 다른 에이전트의 상태를 반복적으로 계산할 필요가 없습니다 (이 논문의 장점). 에이전트 간의 장애물 회피에 대한 그림은 그림 7에 나와 있습니다. 자세한 비교는 Sec.VI에 나와 있습니다. 페이지 제한으로 인해 동적 타당성 및 정적 장애물 회피와 같은 수학적 파생물을 더 이상 제시하지 않습니다. 자세한 내용은 독자들에게 이전 작업을 참조하세요.
5. System Architecture
- 전체 시스템 아키텍처는 그림 8에 나와 있습니다. 이 시스템에서 각 에이전트는 무선 네트워크를 통해 전파되는 궤적을 통해 서로 독립적입니다. 탐색 중에 각 에이전트는 포인트 클라우드와 주행 거리 정보를 획득하여 2D 그리드 맵을 구성합니다. 그런 다음 에이전트는 관찰된 지도를 기반으로 로컬 계획을 수행하고 MPC 컨트롤러에 의해 궤적을 실행합니다[28]. 통신 네트워크는 이 시스템에서 궤적을 브로드캐스트하고 에이전트 간에 타임스탬프를 동기화하는 데 사용됩니다. 식(3)에 나타난 바와 같이 궤적에 대한 정보에는 조각의 계수와 지속 시간만 포함되어 있으며, 이는 현대 무선 네트워크에서는 정보 크기가 작다는 것을 의미합니다. 따라서 당사 시스템에서는 통신 지연을 무시할 수 있습니다 (장점). 포인트 클라우드는 장애물에 대한 고정밀 정보를 제공하는 라이더와 같은 센서의 직접적인 메시지입니다. 우리의 프런트 엔드 계획 알고리즘은 공간-시간적 분해를 기반으로 하기 때문에 동적 장애물의 포인트 클라우드는 특히 로봇이 장애물이 밀집된 환경을 횡단할 때 공간 경로 계획 프로세스를 크게 방해합니다. 다른 에이전트의 포인트 클라우드를 제거하기 위해 방송 궤적을 활용하고 동적 에이전트의 포즈를 계산합니다. 각 에이전트는 볼록 다각형으로 모델링되며 포인트 클라우드의 프레임이 처리됨에 따라 각 포인트가 볼록 다각형에 있는지 확인됩니다. 그렇다면 해당 지점은 동적 장애물로 간주되어 매핑 프로세스에서 제거 (mapping할때 동적 물체 제거 agent Elimination)됩니다. 에이전트를 제거하면 나머지 포인트 클라우드는 정적 장애물에서만 나오므로 경로 계획을 위한 충분한 공간이 확보됩니다. 실시간 성능의 이점을 활용하여 당사 시스템은 빈번한 재계획이 가능합니다. 실행하는 동안 각 에이전트는 정적 및 동적 장애물과의 충돌 검사를 수행합니다. 잠재적인 충돌이 감지되는 즉시 재계획이 처리된 다음 새로운 궤도가 생성되고 동시에 다른 에이전트에게 브로드캐스팅됩니다. 또한 로봇의 모션 일관성을 보장하기 위해 에이전트가 로컬 궤적 길이의 절반을 따라 이동한 경우 재계획이 트리거됩니다 (replanning은 path의 절반을 지나는 시점에 이루어 짐).
Experiments 정리
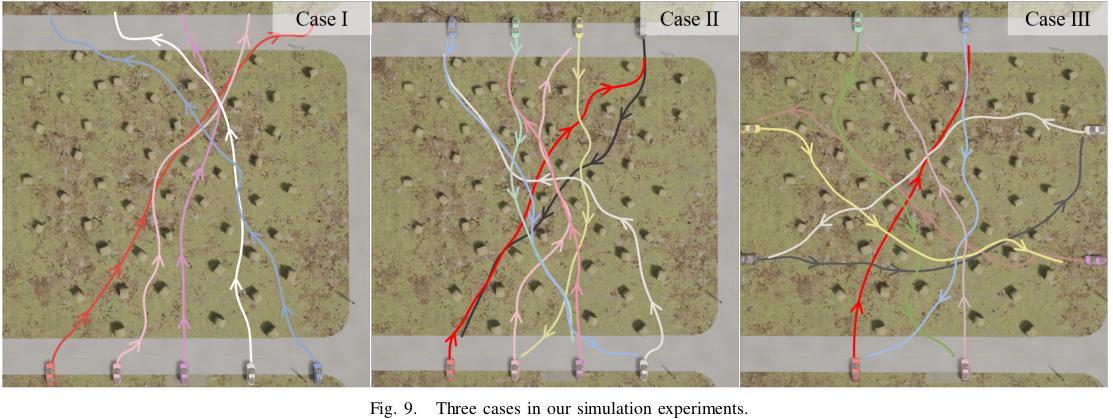
우리는 Carla [2] 및 실제 실험을 통해 시스템의 강인함을 검증합니다. 이 섹션에서는 먼저 시뮬레이션 실험 및 어블레이션 연구를 소개합니다. 그 다음 실제 실험이 제시됩니다.
1) Environment Overview: 시뮬레이션 실험은 장애물이 밀집된 농장 장면에서 수행됩니다. 장면의 크기는 90m × 90m이며, 48개의 장애물이 무작위로 배치되어 있으며, 환경에 대한 사전 정보가 없습니다. 테슬라 모델 3을 차량 모델로 채택하였으며, 최대 속도와 가속도는 각각 8m/s와 3m/s²로 설정됩니다. 3D 라이다는 매핑 센서로 사용되며, 최대 감지 범위는 30m이며, 이는 지역적으로 계획된 궤적의 수평선으로도 사용됩니다. SD-VD 매개변수로는 S = 6m, D = 1.5m를 선택합니다. 테스트된 PC의 CPU는 인텔 코어 i7-10700이며, 16GB RAM이 통합되어 있습니다.
우리는 세 가지 경우를 시뮬레이션합니다: 한쪽에서 다른 쪽으로 이동하는 다섯 대의 차량, 두 쪽에서 서로 반대편으로 이동하는 여덟 대의 차량, 그리고 네 쪽에서 서로 반대편으로 이동하는 여덟 대의 차량이 각각 사례 I, II, III로 표시됩니다. 이는 그림 9에서 볼 수 있습니다.
2) Computation Efficiency Evaluation: 이 시스템의 효율성을 검증하기 위해, 각 모듈에서 소요된 계산 시간을 계산합니다. 또한, 고정된 시간 이산화 전략과 이전 작업의 계산 효율성을 비교하여 개선 사항을 테스트합니다. 평균 계산 시간은 Tab.I에 나열되어 있으며,
3) Ablation Studies: 위상 유도 경로 계획과 검색 기반 속도 계획의 필요성을 평가하기 위해, 위의 세 가지 경우에서 어블레이션 연구를 수행합니다. 각 사례에서 최대 속도를 변화시키며 10번의 시도를 수행하고, 주요 지표는 충돌 없이 성공한 횟수입니다. 위상 유도 경로 찾기 어블레이션의 경우, SD-VD 클래스를 제거하여 궤적 일관성을 취소합니다. 검색 기반 속도 계획 Ablation의 경우, 초기 시간 배치를 제공하기 위해 직접 방방 제어를 채택합니다. 결과는 그림 10에서 볼 수 있으며, TG와 SP는 각각 위상 유도 및 속도 계획을 나타냅니다. 결과는 TG나 SP 없이 성공률이 급격히 떨어지는 것을 명확하게 보여줍니다. 위상 유도 경로 계획 없이는 로봇의 궤적이 빈번한 재계획 하에 동형을 잃고, 에이전트는 어느 쪽으로 이동할지 결정할 수 없어 장애물과 충돌하게 만듭니다. 속도 계획 없이는 초기 값이 나쁜 해의 국소 최소값으로 이어지며, 다른 에이전트와 충돌할 확률이 높아집니다. 결론적으로, 채택된 위상 유도 경로 계획 및 검색 기반 속도 계획은 로봇의 안전성을 효과적으로 보장합니다.
B. Real-world Experiments
3m × 8m 환경에서 실제 실험을 수행합니다. 여기서 세 대의 차량과 같은 로봇이 한쪽에서 다른 쪽으로 이동합니다. 각 로봇은 NVIDIA Jetson Nano를 온보드 프로세서로 탑재하고 있으며, 3m 감지 범위를 가진 단일 라인 라이다를 탑재하고 있습니다. 이는 지역적으로 계획된 궤적의 수평선과 동일합니다. 위치 확인은 NOKOV 모션 캡처 시스템 2에 의해 수행됩니다. WI-FI 모듈은 궤적을 방송하는 데 사용됩니다. 로봇에게는 환경의 사전 지도가 없습니다. 또한, 매핑, 계획 및 제어는 모두 온보드에서 수행됩니다. 최대 속도와 가속도는 각각 0.6m/s와 1.0m/s²로 설정됩니다. 실험은 그림 1에 나와 있습니다. 세 에이전트는 장애물이 풍부한 환경을 통과하는 데 성공하며, 이 과정에서 장애물이 무작위로 이동되어 동적 환경에 대한 강인함을 입증합니다. 실험에 대한 자세한 정보는 첨부된 비디오를 참조하시기 바랍니다.
Conclusion
- 본 논문에서는 복잡한 환경에서 자동차와 같은 Robot swarm을 위한 분산형 프레임워크를 제안합니다. 백엔드 최적화를 위한 실현 가능한 초기값을 제공하기 위해 토폴로지 기반 경로 계획 및 검색 기반 속도 계획이 채택되었습니다. 그 후 안전하고 부드러운 궤적을 생성하기 위해 공간적-시간적 최적화가 사용됩니다. 각 최적화 반복에서 궤적은 고정된 시간 단계로 이산화되어 계산 부담이 줄어듭니다. 실험을 통해 실시간 계획의 높은 효율성과 낮은 충돌 위험이 입증되었습니다. 그러나 교착 상태로 인해 발생하는 몇 가지 문제가 여전히 존재하며, 이로 인해 실험에서 간헐적으로 충돌이 발생하기도 합니다(단점). 앞으로는 부분적인 조정과 그룹 기획을 도입하여 이러한 문제를 해결하도록 노력하겠습니다. 이후 이 프레임워크는 2.5D 환경으로 확장될 예정입니다.



