[Paper Review] 2022_[ICRA]Fast and Optimal Trajectory Planning for Multiple Vehicles in a Nonconvex and Cluttered Environment: Benchmarks, Methodology, and Experiments

 

 

• Video: https://www.bilibili.com/video/BV1k3411q78m/
• Github: https://github.com/libai1943/MVTP_benchmark

【ICRA 2022】复杂非结构化场景中多车协同轨迹规划方法_哔哩哔哩_bilibili

GitHub - libai1943/MVTP_benchmark

Abstract 정리

• multiple car-like robots을 static obstacles 환경에서 cooperative trajectory planning하는데 focused한 논문
• multi-vehicle trajectory planning (MVTP) problem에 주요한 challenges:
  • 시나리오가 nonconvex하고 tiny하다.
  • vehicle kinematics가 nonconvex하다.
  • feasible homotopy class가 unavailable a priori이다. (이게 무슨 말인지 확인 필요)
• two-stage MVTP method를 propose한다.
  • stage 1: identify a feasible homotopy class
  • stage 2: identified homotopy에 base로 하여 local optimum을 찾는다.
• numerical optimal control, adaptive scaling, grouping, and trust region construction straties이 proposed planer에 integrated 되어있다.
• 100가지 benchmark cases에서 SOTA MVTP와 비교하였다.
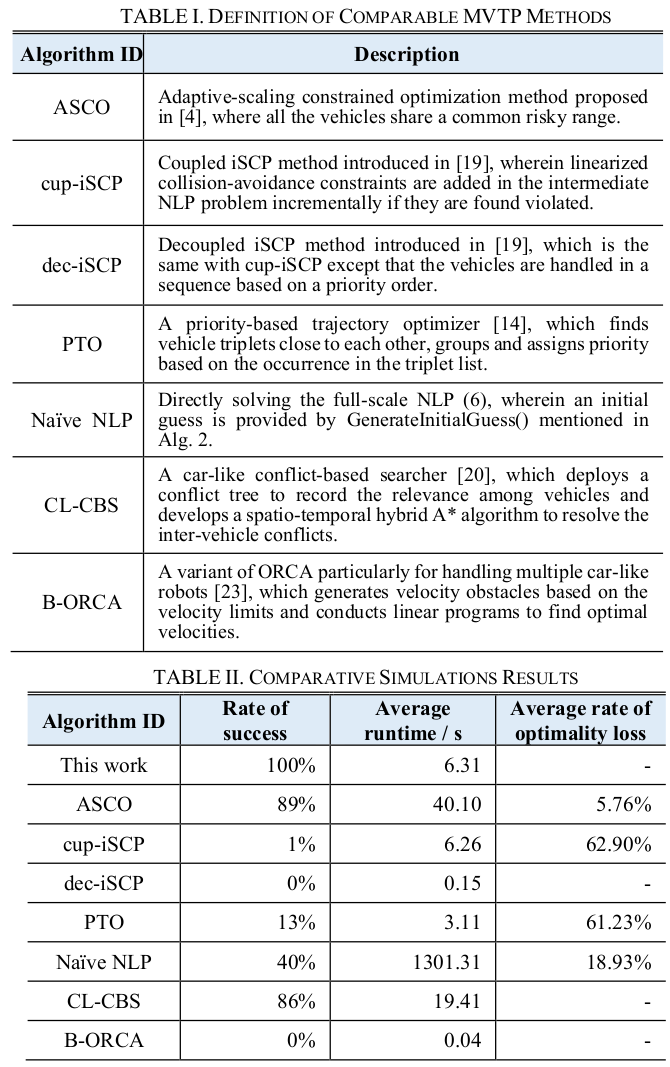
  • 5가지 algorithms: incremental sequential convex programming, numerical optimal control, conflict-based search, priority-based trajectory optimizer, and optimial reciprocal collision avoidance.

---

Introduction 정리

• aerial vehicles에선 MVTP에 관한 연구가 많이 있지만 ground vehicles에서는 몇가지 challenging한 부분때문에 더 어려움
  • ground vehicles은 static obs에 의해 2차원 narrowed space에서 planning 해야함.
  • vehicle kinematics가 nonconvex임.
• ground-vehicle-based MVTP problems은 structed scenarios보다 unstructured scenario에서 더 어려운데 그 이유는 inter-vehicle conflicts가 entir time horizon에서 strong throughout이기 때문이다. (Fig. 1 참조)

• 이 study는 static obs에 의해 occupied된 cluttered indoor 환경에서 swarm of vehicles를 위해 fast and optimal MVTP solutions을 찾는 것이 목적이다. (이 논문의 목적)

---

Related Works 정리

• existing MVTP methods는 coupled와 decoupled로 구분되어진다.
  • coupled method는 모든 vehicles을 integrated system으로 여기고 동시에 그들의 trajectories을 생성한다. Mixed-integer linear program (MILP), mixed-integer quadratic program (MIQP), and nonlinear program (NLP)들이 typical한 coupled MVTP problem forms이다. coupled method는 cooperation potentials을 exploit할 수 있지만 large vehicle swarms을 다룰 수 없는데 그 이유는 inter-vehicle collision-avoidance constraints의 dimension이 vehicles의 수에 따라 scale이 어렵기 때문이다.
  • decoupled method는 coupled problem을 쉬운 subproblems로 나누고 gradually 정복한다. 주로 decoupling strategies은 prioritization, grouping, tube construction, prediction, and constraint reduction을 포함한다.
    • prioritization-based method는 vehicle team을 위해 priority order를 assign하는데 single-vehicle trajectories을 plan하고 planned trajectories을 각각의 low-priority vehicle에 따라 moving obstacles로 보고 fix한다. 이 방법의 단점은 만약 priority order가 poorly defined 되었다면 deadlocks을 일으킬 수 있다.
    • grouping-based planner는 vehicle team을 isolated subgroups로 나누는데 각각의 subgroup들에 따라 cooperative trajectories을 plan하고 complete solution을 만들기 위해 subgroups사이의 obtained trajectories을 combine한다. 이 방법의 단점은 tiny scenario에서 vehicles이 서로 가까우면 inefficient하다.
    • tube contruction method는 만약 각각의 vehicle이 corridor안에 있고 surrounding obstacles와 naturally 떨어져 있다는 가정하에 safe corridor를 생성한다. sequential convex program (SCP)-based method는 tube construction 범주에 속하는데 이 방법은 몇몇 half-planes의 intersection안에 각각의 vehicle을 stay하게 ensure하기 위하여 collision-avoidance constraints를 linearize하기 때문이다. (hyper plane constraints을 써서 optimization하는 방법을 말하는 것 같음.) 일반적으로, reference trajectories이 safe corridors을 paving하기 위해 skeletons으로 사용되기 때문에 중요하고, 그러므로 final output을 strictly homotopic하게 만든다. collision-avoidance constraints을 linearize하기 위하여 SCP-based method하에서 reference trajectories이 first-order Taylor expansion points로서 사용되는 조건하에, 이 고안된 solution의 homotopy class는 reference trajectories과 일치한다. 단점은 multi-agent path finder (MAPF)와 conflict-based searcher (CBS)같은 Grid-based methods은 배포되어 satisfactory reference trajectories을 제공한다. 그럼에도 불구하고, 이러한 reference trajectories에 대한 지나친 의존은 만약 reference trajectories이 homotopically misleading된다면 쉽게 trouble에 빠질 수 있다. 
    • prediction-based method은 각각의 agent가 forward propagation을 통해 other agents의 motions을 predict하고 other agents의 predicted motions을 피하기 위해 각자 trajectory를 plan한다. 단점은 이 prediction이 항상 accurate하지 않다면, 이리 언급한 process는 convergence하기까지 반복적으로 repeated 되야만 한다. typical prediction-based methods은 distributed model predictive controller (DMPC)와 optimal reciprocal collsion avoidance (ORCA)가 있다. 이 방법은 매우 빠른데 each agent의 planning procedure가 parallel하게 생성되기 때문이다. 하지만, DMPC는 inter-vehicle conflicts가 harsh할 경우 converge하기 위해 지나치게 많은 iterations이 필요로 한다. ORCA-based methods에 의해 생성된 results은 endpoint orientation-angle constraints을 만족시키지 않는데; highly nonlinear vehicle kinematics는 또한 MVTP problem을 복잡하게 만든다. 전반적으로, prediction-based methods은 scenarios과 vehicle kinematics가 complated하다면 빠르게 동작하지 않는다. (section 6에서 validated)
    • constraint-reduction-based method는 일시적으로 difficult constraints을 지우고 gradually 더해가는 방법이다. [26] 논문에서 optimal control problems (OCPs)를 순차적으로 풀었는데 처음에 모든 inter-vehicle collision-avoidance constraints이 discarded되었고; iterations동안 그것들이 intermediate OCPs로 더해졌다; 한 interation에서의 optimum은 다음 iteration의 initial geuss 역할을 합니다. 하지만, 이 방법은 만약 inappropriate을 찾는다면 homotopy class를 긍정적으로 바꿀수 없고, iteration process는 harsh cases에서 쉽게 stuck에 빠집니다. [19]는 incremental Sequential Convex Program (iSCP) method를 제안하는데 이는 각각의 intermediate problem을 enhance하기 위해 linearized collison-avoidance constraints을 incrementally adds/updates 합니다. 하지만, 이 방법은 complexity of kinematics and scenarios 때문에 각각의 intermediate QP problem이 항상 feasible하다고 보장할 수 없습니다. adaptive-scaling constrainted optimization (ASCO) method는 collision-avoidance constraints가 ring-like risky range에서 only activate되고 lower와 upper bounds가 adaptively change합니다. circle보다 ring으로 risky range를 setting하는 것은 innovative idea인데 close-range collision-avoidance constraints을 discarding하게 해주기 때문이고 이건 다른 homotopy class로 switch하는 기회를 가져다 줍니다. 이 방법은 good homotopy class가 a priori를 identified 할 수 없는 경우를 handling하게 만들 수 있지만, runtime이 여전히 느린데 이는 모든 vehicles이 risky range를 공동으로 share하고 있기 때문이다. 이건 각각의 vehicles의 차이점들이 무시된다는 의미이다.
    • 특히, 언급한 coupled와 decoupled strategies은 planning efficiency를 향상시키기위해 혼합된다. 예를들어 [19]은 tube construction과 constraint reduction 방법을 combine하고 [14]는 priorization, grouping, and tube construction 방법들을 combine한다. 그럼에도 불구하고, existing MVTP방법들은 여전히 low success rate과 run slowly한데 environment가 tiny하고 vehicle의 갯수가 많은경우에 그렇다.

Motivations, contributions, and organization

• 이 논문은 cluttered 환경에서 많은 car-like robots이 fast하고 cooperative trajectories을 plan하는데 목적으로 한다.
• optima를 찾기위해 MVTP problem은 coupled OCP로 formulate되어야하고 numerically 풀어야한다. 하지만, coupled OCP는 어쩔 수 없이 numerical solution process가 느려지게하는 다루기 힘든 scaled inter-vehicle collision-avoidance constraints를 가지고 있다. 한가지는 decoupled 방법이 선택되어야 하는데 앞서 언급했다시피 이는 completeness, optimality, and robustness w.r.t. initial guess에 관해서 imperfect하다. 언급된 사실들이 주어진다면, 명목상 coupled OCP를 formulate하고 mix of several decoupled strategies을 solve한다. 하지만, coupled OCP의 optimum을 고안하는 목적이 있고 이 idea는 만약 mixed decoupled strategies(주된 방법론)이 간단하게 intractable collision-avoidance constraints과 nonconvex kinematic constraints (이것들은 coupled OCP의 주된 어려움들이다.)을 간단하게 하는데 도움을 준다면 solution optimality와 speed를 보장하는데 promising하다. (무슨 말인지 이해 잘 안됨) constraint simplification은 주로 good initial guess에 기반을 두는데 이는 실제로 homotopy class를 반영하는 coarse solution이다. (i.e., other vehicles와 static obstacles의 어느 isde로 지나갈지에 대한). single-vehicle trajectory planning과 반대되게, sampling-/search-based planners은 curse of dimensionality 때문에 적절한 homotopy class를 initial guess로 주지 못한다. 좋은 homotopic class를 가진 initial guess는  a priori로 identified되기 쉽지 않다는 것을 인정함으로써, [4]와 같은 initial-guess-intensive method를 building하는 것을 고려한다. 하지만, [4]는 여전히 느린데 그 이유는 같은 속도로 모든 vehicles의 risk range를 조절해서 flexibility가 부족하기 때문이다.
• 이 연구의 contribution은 run fast하고 optimum을 찾는 two-stage MVTP method를 제안하는 것이다.
• Stage 1은 grouping, tube contruction, and diversified ASCO와 같은 decoupled strategies이 결합되어 trial and error process를 서두르는 동안에 interative loop으로 trial and error를 통해 feasible homotopy class를 찾는다..
• Stage 2는 identified homotopy class를 기반으로 local optimum을 찾는다.
• 주목할 점은, proposed planner는 community에서 찾을 수 있는 거의 모든 competitors과 비교되었다.

---

Methodology 정리

Problem Statement

coupled OCP는 multiple car-like robots이 time-energy-optimal demand에 따라 충돌없이 그들의 goal에 동시에 도착합니다.

(Problem statement의 경우 논문 내용만 참고)

The proposed MVTP method

A. Overall Framework

• task는 each vehicle에 assign된 initial/terminal poses를 record하고 map은 scenario size와 obstacle locations을 record. MVTP()의 final output은 each vehicle의 optimized trajectory를 record.

B. Stage1: Identify a Valid Homotopy Clasds

• Stage1은 GenerateInitialGuess()를 이용하여 $N_V$ vehicles의 trajectories을 구성하는 initial guess를 처음에 찾는다. static obstacles로부터 빠르게 collision-free path를 찾기 위해서 fault-tolerant hybrid A*(FTHA)[29]를 이용하고 min-time velocity profile [30]이 이 path에 생성된다. $\text{T}_\text{max}$는 충북히 큰 시간으로 parameter 설정을 하고, 모든 vehicles의 goal 도착 시간을 $t=\text{T}_\text{max}$로 맞추기위해 모든 vehicles의 속도를 proportionally relax한다 [19]. 각각의 trajectory가 $t=0$부터 $\text{T}_\text{max}$까지 state/control profiles을 evenly sampled하여 $TRAJ=\{traj_1, traj_2, \ldots, traj_{N_V} \}$로 initial guess를 나타낸다.
• Remark 1. GenerateInitialGuess()는 inter-vehicle collisions을 무시하기 때문에 homotopy class는 infeasible할 수 있다. 그래서 further corrected가 필요할 수 있다.
  • Alg.2의 while loop동안에, DivideGroups()에 의해 entire vehicle team이 subgroups로 divided된다. 구체적으로, 이 vehicles은 $TRAJ$에 따라 travel한다고 가정한다. 모든 two vehicles $i$와 $j$의 mutual min-distance가 two intervals $[S_\text{lb}[i], S_\text{ub}[i]]$ 와 $[S_\text{lb}[j], S_\text{ub}[j]]$ 에 걸쳐 속하는지 확인합니다. 만약 true라면, vehicles $i$와 $j$가 relevant하다고 여겨진다. 여기서, $[S_\text{lb}[i], S_\text{ub}[i]]$는 충돌 위험이 일시적으로 무시되는 vehicle $i$의 risky range라고 여겨집니다 [4]. $\{1, \ldots, \text{N}_\text{V}$의 모든 two vehicles을 열거한 후, 한 subgroup의 any vehicle이 다른 subgroup의 any vehicle에 relavant하지 않도록 whole vehicle team을 독립적인 subgroup으로 cluster할 수 있습니다. (관계가 서로 없는 vehicles을 subgroup으로 clustering을 하기 위한것). Alg. 2의 line 5-21은 $list$라는 subgroup안에 vehicles에 대해 trajectories이 plan 된다. 각각의 vehicle $id \in list$에 대해, initially guessed trajectory $traj_{id}$가 $TRAJ$로 부터 extracted되고 모든 $\text{N}_\text{FE}+1$ 시간동안 모든 K instances의 surroundings과의 min-distances가 check된다. range $[S_\text{lb}[id], S_\text{ub}[id]]$안에 min-diance가 들어올 때마다, vehicle-to-vehicle 혹은 vehicle-to-obstacle collision-avoidance constraints가 constraints (line 9)에 더해진다. (collision constraint 생성). subgroup의 모든 vehicles을 열거한 후, small-scale NLP problem이 BuildNLP()에 의해 concerned subgroup으로 formulated된다. $NLP_\text{subtle}$ (line 11)에서는, constraints에서 recorded된 collision-avoidance constraints만 모든 $K$ instances로 $[0,T]$에 따라 imposed된다. 게다가, 각각의 vehicle에 imposed된 front/rear discs이 initial guess로 부터 너무 많이 drift되지 않도록 ensure한다: (NLP 생성)

• -
  
  • $NLP_\text{subtle}$이 formulated후, gradient-based solver로 solve된다. solution process가 성공하면, 이 derived trajectories이 $TRAJ$ (line 16)에서 recorded된 $TRAJ$을 대체한다. 또한, $sol$에 있는 each trajectory가 모든 $K$ instances의 $constraint$에서 무시됐던 close-range collisions을 포함하는지 check한다. 특히, close-range collisions은 단지 그들이 risky range안에 없을 경우에만 일어나기 때문에, $S_\text{lb}[id]$는 future iteration에서 $NLP_\text{subtle}$의 more collision-avoidance constraints을 collect하기를 바라면서 더 작게 set될 자격이 있다 (line 18). 반대로, solution process가 실패한다면, concerned subgroup의 모든 vehicles이 $S_\text{lb}[id]$를 증가시킴으로써 그들의 risky ranges을 줄여야한다 (line 14). 이러한 경우에, 더 적은 collision-avoidance constraints가 포함되기 때문에 next-iteration NLP solution process가 더 쉬워진다.
• Remark 2. closed-range collisions은 각 vehicle의 risk range의 lower bound (i.e., $S_\text{lb}[id]$)가 positive나 large로 설정되었을때 의도적으로 무시된다. 이건 다른 homotopy class로 switch하기 위해 변화를 가져온다.
• Remark 3. line 5-21의 for loops은 subgroups이 independent하기 때문에 시간을 절약하기 위해 parallel로 실행될 수 있다. 모든 subgroups이 실행된 후, line 22에서 $TRAJ$의 inter-subgroup collision을 check한다. 단지 minor collisions (line 3)가 존재한다면, 최근 $TRAJ$로 Stage 1이 종료되고 그렇지 않다면, $S_\text{ub}[i]$를 증가시키고 $S_\text{lb}[i]$를 감소시켜서 risky range를 확장시킨다 (line 23).
• Remark 4. inter-vhiecle collisions이 subgroup에서 발견되면 (line 17), trust resions (7)이 imposed되어 distant collisions이 거의 일어나지 않기 때문에 large $S_{lb}[id]$를 이용하는게 reasonable해 보인다. 이게 line 18에서 $S_\text{ub}[id]$를 증가시키는 대신에 단지 $S_\text{lb}[id]$를 감소시키는 이유다. line 22에서 inter-subgroup collisions이 발견되면, line 23에서는 양쪽끝에서 expansion이 일어난다.

C. Stage2: Calculate Optimal Trajectories

• near-feasible solution $TRAJ$인 Stage1의 outputs을 Stage2에서 polish하여 optimal one으로 만든다. Stage 2의 목적은 subgroups로 decouple하지 않고 nominal problem (1)의 local optimum을 찾는 것이다. 하지만 여전히, 꽤 좋은 $TRAJ$가 stage 2의 처음에 가능하기 때문에 (1)의 해결하기 어려운 constraints을 단순화하길 원한다.

• Alg. 2와 비슷하게, Alg. 3는 intermediate NLPs가 반복적으로 solve되는 while loop로 구성된다. stage 3의 새로운 features은 뒤에 listed된다.
  • 첫째, 모든 vehicles의 trajectories을 동시에 plan하기 위해서 더이상 grouping은 필요로 하지 않는다.
  • 둘째, Alg.2에서 vehicles의 risky ranges을 받는데, Stage 2에서는 더이상 homotopy class를 바꿀 필요가 없기 때문에 각 $S_\text{lb}[i]$는 0으로 fixed된다.
  • 셋째, terminal time $T$는 더이상 $NLP_\text{gross}$로 fixed되지 않는다.
  • 넷째, $K$는 1로 fix된다. 이건 any collocation instance에서도 collision-avoidance를 더이상 skip하지 않는다는 의미이다.
  • 다섯째, 일단 intermediate solution이 실패하면, 전체 algorithm이 실패한다.
  • 여섯째, while loop은 모든 시간구간동안 모든 collision-avoidance constraints가 만족할때까지 계속된다.
  • 일곱째, interation이 계속되면서 risky ranges의 upper bounds는 monotonically 증가한다.
• Remark 5. 경험적으로, stage2는 $NLP_\text{gross}$의 scale이 first few iterations에서 크지 않기기 때문에 빠르다. trust region constraints (7)이 여전히 존재하기 때문에, converges는 iterations동안에 많은 adjusting efforts가 없이 달성된다.
• source code is available at https://github.com/libai1943/MVTP_benchmark.

---

Experiments 정리

• (작성중)

 

 

---