Collaborative Planning for Catching and Transporting Objects in Unstructured ..._哔哩哔哩_bilibili
Video for the RAL submission. Title: Collaborative Planning for Catching and Transporting Objects in Unstructured Environments Preprint: https://arxiv.org/abs/2311.07100 BGM: Diamond - Klint (盖里奇导演的《Snatch》的片头曲)
www.bilibili.com
Abstract 정리
- 다중 로봇 팀은 황야 구조, 협동 운송 등 비정형 환경에서 협업 작업을 수행하는 능력으로 업계와 학계의 주목을 받았습니다. 이 letter에서 우리는 구조화되지 않은 환경에서 협업을 통해 비홀로노믹 로봇 팀을 위한 궤적 계획 방법을 제안합니다. 그물을 이용하여 구조할 표적을 잡아 운반하는 로봇팀의 적응형 상태 협업을 위해, 떨어지는 표적을 그물로 잡는 과정을 연속적이고 미분 가능한 형태로 모델링한다. 이를 통해 로봇 팀은 운동학적 잠재력을 완전히 활용하여 적절한 상태에서 대상을 적응적으로 잡을 수 있습니다. 또한 로봇의 협업 지원으로 인한 네트의 크기 안전성과 위상학적 안전성은 기하학적 제약을 통해 보장됩니다. 우리는 자동차와 같은 로봇 팀에 알고리즘을 통합하고 이를 시뮬레이션과 실제 실험에서 테스트하여 성능을 검증합니다. 우리의 방법은 최첨단 다중 차량 궤도 계획 방법과 비교되어 효율성과 궤도 품질에서 상당한 성능을 보여줍니다.
Introduction 정리
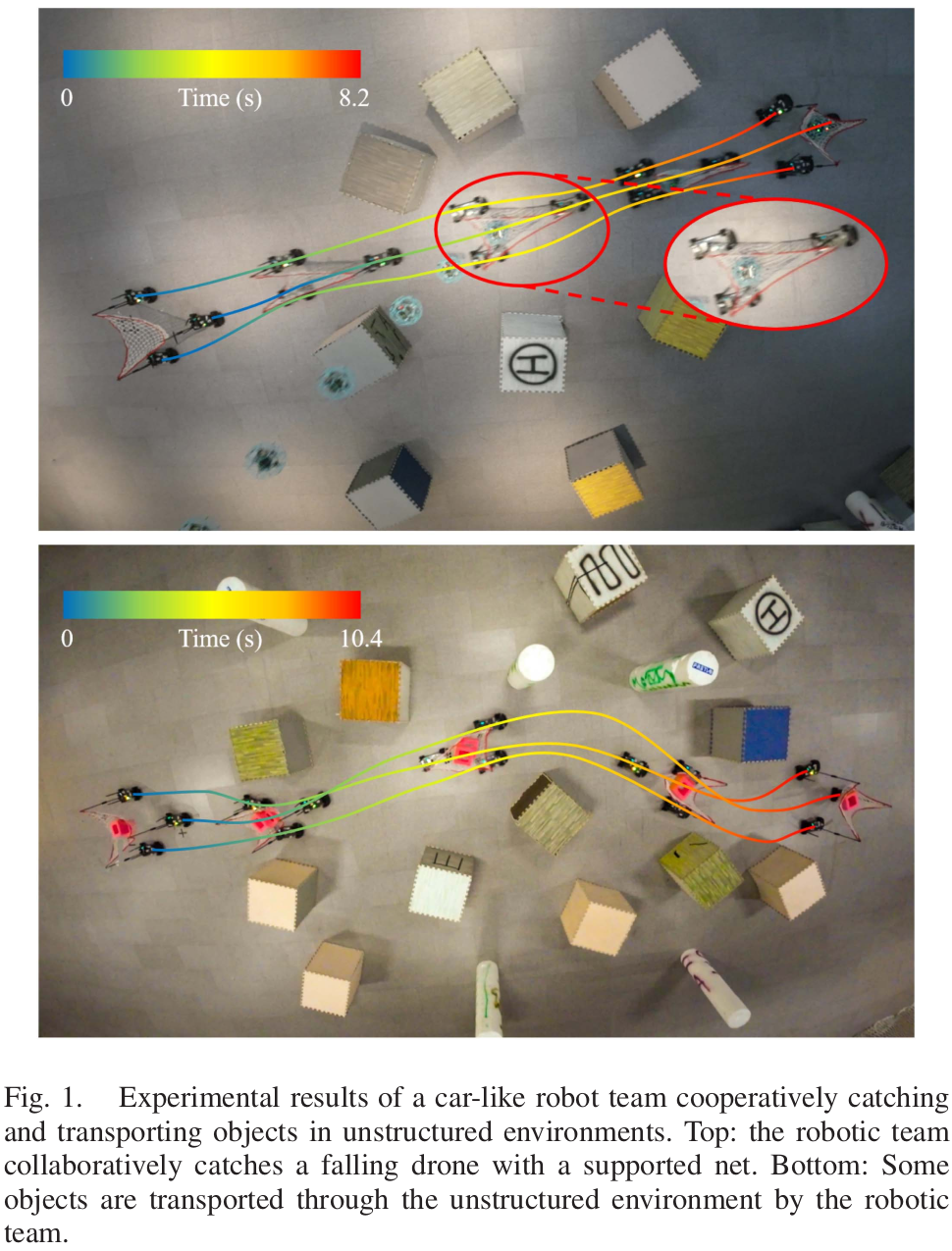
- collaborative catching과 transportation tasks을 위해, 추가로 individual motion constraints와 obstacle avoidance를 고려하고 robotic teams사이의 정확하고 효율적인 collaborative relationships을 모델링하는 것은 매우 중요하다.
- 첫째로, rescue target이 떨어질때, robot team이 이론적으로 feasible한 state에서 target을 잡는게 필요하다 (adaptive catching). 그래서 target을 잡을때 team formation의 state는 환경과 target까지의 거리에 따라 조정되어야한다.
- 둘째로, trajectories은 모든 순간에 피로 및 손상 범위내에서 그물의 물리적 크기를 유지해야합니다. (size safety). 모든 순간에, 어느 두 로봇사이의 거리는 distance limit을 벗어나면 안된다.
- 셋째로, 그물의 edges은 어떠한 agent에 의해서도 얽혀서는 안됩니다. (topological safety). 어느 시점에서도, 두 다른 로봇들에의해 supported되는 그물의 edge를 통과해서는 안된다.
- collaborative relationships의 구현은 time과 space관점에서 great demand하고 그로 인해서, high-dimensional and strongly non-convex problem가 생성된다. 하지만, 현재까지의 existing method는 catching과 transporting tasks를 online으로 완료할 수 있는 non-holonomic robot teams의 trajectory planning 방법은 없다.
- 이 논문에서는 car-like robotic teams을 위해 efficient centralized planning framework를 제안한다. 이 framework를 기반으로, any feasible robot formation을 위해 optimization에서 fast gradient descent를 가능하게하는 continuous하고 differentiable한 form을 modeling한다. 그 결과로, 이 robot team은 target을 잡기위해 이 potential을 fully 활용하여 더 적절한 state로 deforming할 수 있게한다. 추가로, formation relationship을 modeling 함으로써 그물의 사이즈와 team formation의 topology에 제약조건을 부과한다. rescue net의 size safety와 topological safety는 navigation 동안 guarantee된다. 게다가, 효율적인 trajectory representation과 optimization의 decision variables transformation 덕분에, robot team이 적절하고 정확하게 catching과 transporting tasks을 수행하게 만드는 trajectories planning이 효과적으로 online으로 완료될 수 있다.
Controbutions
- kinodynamic feasibility 와 함께 unstructured environments에서 safe trajectories 생성을 가능하게 하는 효율적인 collaborative car-like robot team planning을 제안한다.
- real-time collaborative catching과 transporting planning을 위해, multiple essential collaboration relationships을 modeling하고 이 framework를 기반으로 구현했다.
- proposed method를 car-like robot team에 통합하고 simulation과 real-world에서 검증했다.
Related Works 정리
- 최근 MVTP 문제들은 coupled method에서 decoupled methos로 decompose하여 enormous scale을 낮춰서 해결하고있다. [8]는 prioritized trajectory optimization방법을 제시하는데 enhanced conflict-based search (ECBS)[9]를 이용하여 initial collision-freee paths을 얻고 이 paths에 따라 safe corridors을 생성한다. 이것들은 grouping 전략을 통해서 전반적인 solution efficiency를 향상시켰다. initial trajectory로부터 벗어나는데 드는 penalty cost는 optimization의 성공률을 위해 소개되는데 이는 solution space를 상당히 제한시킨다. 게다가 sequential optimization은 dense한 환경에서 deadlock을 일으킨다. [7]은 distributed model predictive control (DMPC) 기반의 multi-agent motion planning framework이고 free space를 위해 덜 보수적인 movement와 빠른 transition times를 가진 real-time trajectory planning이 가능하게 하는 collision avoidance를 사용했다. 하지만, DMPC는 특정 horizon영역에서만 planning하도록 focused 되어있는데 이는 agents의 complete trajectories이 종종 optimal하지 않을 수 있다는 의미이다.
- multiple agents의 future states를 고려하기위해, centralized methods는 모든 agents의 trajectories을 하나의 문제로 푸는 방법이다. [6]은 collision constraints을 incrementally tightening하여 MVTP 문제를 푸는 방법이고, 이는 더 relaxed하고 feasible한 intermediate optimization problems의 sequence를 만든다. 이 방법들은 agents을 avoidance를 위해 circles로 여기는 보수적인 방법들을 사용하는데, 이는 kinematics가 complex할때 QP문제가 풀린다는 것을 guarantee하지 않을 수 있다. [10]은 adaptive-scaling contrained optimization (ASCO)를 제안하는데, 이는 다루기 어려운 scaled constraints을 coupled OCP로 나누고 iterative framework로 정복한다. 각각의 iteration에서, partial collision avoidance constraints은 adaptive range안에서 구현된다. [5]는 two-stage method를 제안하는데, 이는 feasible homotopy class를 찾아내고 이 찾아낸 homotopy class를 base로 하여 local optimum을 찾아낸다 (이전 포스팅에서 소개한 논문). 하지만, 이 논문에서는 car-like robot을 두개의 circles로 obstacle avoidance를 위하여 나타내고 (보수적이다.) problem이 dense states을 real-time performance를 guarantee하기 어려운 optimization variables로 사용한다. [3, 11]은 Car-like Conflict-based Search (CL-CBS)라고 불리는 hierarchical search-based solver를 소개하는데 이는 non-holonomic kinematic models을 위해 spatiotemporal hybrid state A*를 제안하는 방법이고 agents의 shapes을 고려하여 collisions을 다루기위해 body conflict tree를 적용하였다.
Methodology 정리
Collaborative Trajectories Optimization
car-like robots[12]의 motion model과 differential flatness property를 소개하고 collaborative planning을 optimization problem으로 formulation한다. 그리고 나서 constraint (basic kinematic constraints와 environmental obstacle avoidance constraints for agents) handling approach를 소개한다.
A. Differential Flatness of the Car-Like Robots
- car-like robots의 kinematics를 표현하기위해 cartesian coordinate frame에서 simplied kinematic bicycle model을 사용한다. 이 차는 front-wheel driven이고 steered with perfect rollising이며 no slipping이라고 가정한다.

- state vector는 $\textbf{x} = (p_x, p_y, \theta, v, a_t, a_n, \phi, \kappa)^{T}$.
B. Optimization Problem Formulation
C. Single Agent Constraints
1) Kinodynamic Constraints:
2) Environmental Obstacle Avoidance:
Collaboratively Catching and Transporting Objects
A. Inter-Agents Obstacle Avoidance
B. Collaborative Transportation
C. Adaptive Catching
Experiments 정리
A. Benchmark Comparisons
- 제안한 방법의 효율성과 계산 효율성을 검증하기 위해 이를 여러 최신 MVTP 방법과 비교했습니다. 모든 방법은 32GB 메모리를 갖춘 Intel i7-12700 CPU에서 테스트되었습니다. 우리는 무작위 크기와 위치의 장애물 8개를 사용하여 100개 사례에 대해 테스트를 수행했습니다. 비교 실험의 공정성을 보장하기 위해 Hybird A* 알고리즘을 사용한 방법에 대해 동일한 초기 추측을 제공했습니다 [17]. 자세한 내용은 보충 자료 [16]의 섹션 7에 소개되어 있습니다. 다양한 수의 에이전트를 테스트하고 성공률, 계산 시간, 에이전트 궤적을 실행하는 평균 시간, 가장 긴 궤적을 실행하는 평균 시간, 평균 총 궤적 길이 및 평균 궤적 가속 비용을 기록했습니다. 이러한 결과는 Table 1과 같다. 데이터를 보면 FOTP가 높은 성공률을 보이나, 궤적 내 모든 상태와 입력의 조밀한 결정 변수로 인해 문제 차원이 극도로 높아 엄청난 문제가 발생함을 알 수 있다. 계산 부담. 대조적으로, 우리가 제안한 방법은 다항식 궤적의 각 부분의 중간점과 지속 시간을 최적화하여 FOTP에 비해 계산 시간이 크게 향상됩니다. 반면, 제안한 방법은 충돌 회피를 고려하지 않고 초기 경로만 개선하면 비교적 짧은 시간에 에이전트 간 충돌 회피를 완료할 수 있으므로 초기 경로에 대한 의존도가 크게 줄어듭니다 (장점). MNHP 방법은 그룹화 및 우선 순위 전략과 함께 분산 접근 방식을 사용합니다. 그러나 이와 관련된 몇 가지 제한 사항이 있습니다. 첫째, 장애물 회피를 위해 로봇을 원형으로 간주하는데, 이는 보수적이며 솔루션 공간이 줄어듭니다. 이러한 제한은 로봇의 모양을 고려해야 하는 환경, 특히 로봇의 모양이 중요한 좁은 공간에서 효율성을 저하시킵니다(MNHP방법의 단점1). 둘째, MNHP 방법은 비용 함수에서 ECBS[9]가 제공한 초기 값에서 궤도가 벗어나는 정도에 페널티를 적용합니다. 초기 값에 대한 이러한 과도한 의존성은 성능에 큰 영향을 미칩니다 (MNHP방법의 단점2). 테스트 결과, 이 비용 구성요소의 가중치가 0으로 설정되었을 때 MNHP는 에이전트 간 충돌 방지를 달성하는 데 어려움을 겪는 것으로 나타났습니다. 셋째, MNHP는 궤적 시간을 최적화하지 않으며 모든 에이전트가 지정된 최종 상태에 동시에 도달해야 합니다. 이러한 제약은 성공적인 안뜰시간적 충돌 회피 가능성을 더욱 감소시킵니다(MNHP방법의 단점3). 이러한 세 가지 제한 사항은 종합적으로 MNHP의 효율성을 제한합니다. DMPC는 우선순위 기반 전략을 사용하고 주문형 장애물 회피 전략을 사용합니다. 그러나 각 계획 반복마다 가까운 미래의 지역 정보만 고려하므로 지나치게 탐욕스러운 행동과 낮은 궤적 품질로 이어집니다. 장애물과 에이전트가 밀집된 지역에서는 우회하는 경우가 많으며, 탐욕으로 인해 실행 불가능한 상황에 갇힐 수도 있습니다. 이러한 모든 요인으로 인해 DMPC의 낮은 성공률과 긴 이동 거리가 발생합니다(DMPC의 단점). 대조적으로, 우리의 결합 방법은 DMPC에 비해 계산 효율성에서 상당한 이점을 유지하면서 더 높은 솔루션 품질과 성공률을 제공합니다. 데이터에서 CL-CBS는 성공률이 높지만 원활성에 영향을 주지 않고 실행 가능한 솔루션 역할을 할 수 있는 시간 순서의 경로만 제공한다는 것을 알 수 있습니다. 더욱이 솔루션을 찾는 데 있어서 semi-decentralized approach으로 인해 지속적으로 축소되는 솔루션 공간에서 계산 시간이 급격히 증가하고 궤적 품질이 더 낮은 우선 순위 에이전트의 문제에 직면합니다(CL-CBS의 단점; 왜 semi-decentralized approach가 지속적으로 솔루션 공간을 축소??). 그림 5와 같이 에이전트 수를 계획하는 다양한 경우에 대해 표에서 가장 성공률이 높은 두 가지 방법인 FOTP와 CL-CBS에 대해 테스트를 수행했습니다. 에이전트 수가 증가할수록, 제안하는 방법의 계산 시간은 다른 방법에 비해 작은 크기로 점차 증가한다. 그러나 역시 최적화를 기반으로 하는 FOTP는 35개 에이전트 이후 1000초가 넘는 계산 시간에 도달합니다.
B. Real-World Experiments
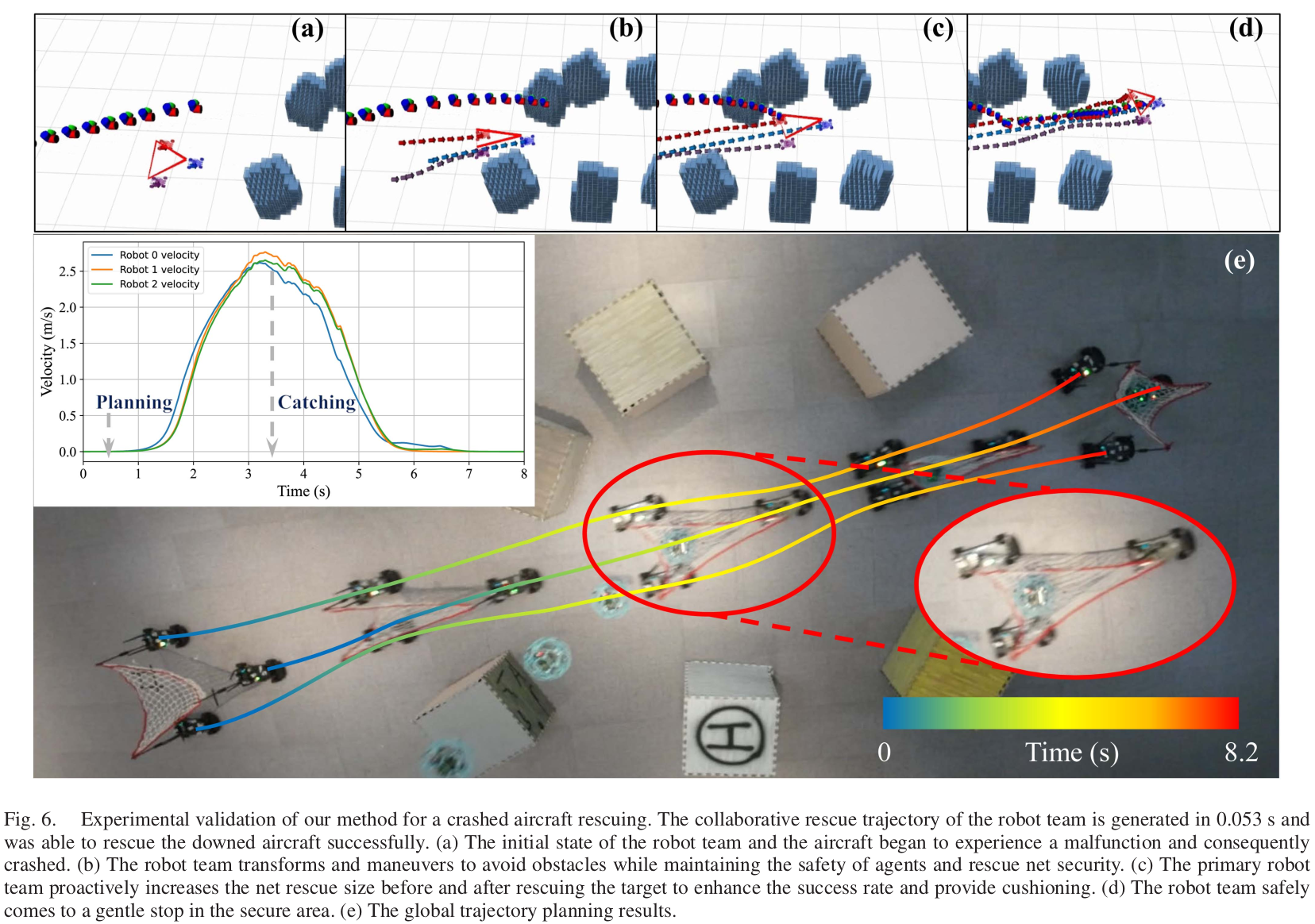
- 실험 필드는 무작위 장애물이 있는 6m x 12m 필드이며 로봇은 협력하여 그물을 지원합니다. 중앙 계획 플랫폼의 프로세서는 16GB RAM을 갖춘 8세대 Intel i5-8700이며, 궤적은 온라인 추적을 위해 떼 에이전트로 전송됩니다. 우리는 자동차 형태의 로봇 3대 각각의 후면에 그물의 꼭지점을 고정하고 현장에서 공동 운송 실험을 수행합니다. 목표 상태가 주어진 후 중앙 컴퓨팅 플랫폼은 로봇 팀의 궤적을 계산하고 각 에이전트의 MPC 컨트롤러가 뒤따릅니다[23]. MPC는 실험 로봇의 시공간 궤적을 제어하기 위한 일반적인 궤적 추적기 역할을 합니다. (1)에서 소개된 것과 동일한 모델을 활용하며 제안된 방법으로 생성된 로봇 팀 궤적을 입력으로 사용합니다. 추가 적용 세부사항은 보충 자료의 섹션 III에 소개되어 있습니다[16]. 포획 과정은 그림 6에 나타나 있으며, 실패한 드론이 구조 대상 역할을 한다. 비행 중 드론이 갑자기 오작동을 일으키며 추락했습니다. 드론이 추락할 것으로 예상되는 위치와 시간을 얻었다고 가정하면 시스템은 협력적인 구조 궤적을 계획하기 시작합니다. 우리의 방법은 단 0.053초 만에 세 대의 자동차 같은 로봇에 대한 협업 궤적을 생성합니다. 이 과정에서 각 에이전트의 움직임의 기구학과 안전성을 만족시키는 것 외에도 네트의 크기 안전성과 위상학적 안전성도 모두 보장됩니다. 생성된 궤적은 구조 임무를 완료하기 위해 로봇의 운동학적 성능을 최대한 활용합니다. 그림 6(e)와 같이 장거리 구조를 성공적으로 수행하기 위해 로봇팀은 먼저 거의 최대 가속도로 가속한 후 거의 최대 속도로 구조를 달성한다. 그러다가 후단의 종말상태가 완화되면서 안전지역에 원활하게 정지하게 된다.
Conclusion
- 이 작업에서는 공동 목표 포착 및 운반 기능을 갖춘 공동 로봇 팀 계획 시스템을 소개합니다. 협동 작업을 모델링함으로써 우리는 물체를 협동적으로 잡고 운반하는 자동차와 같은 로봇 팀의 계획을 완성합니다. 현재의 여러 MVTP 방법과의 비교는 우리 방법의 솔루션 품질과 확장성을 보여줍니다. 시뮬레이션과 실제 실험은 우리 방법의 견고성과 유연성을 보여줍니다. 앞으로 연구 방향 중 하나는 우리의 방법을 3차원 환경에서의 운송으로 확장하는 것입니다. 여기서 팀 구성은 운송물이 높이를 고려한 장애물을 피할 수 있도록 변경됩니다.



